
Question Number 128617 by ajfour last updated on 08/Jan/21
Commented by ajfour last updated on 08/Jan/21
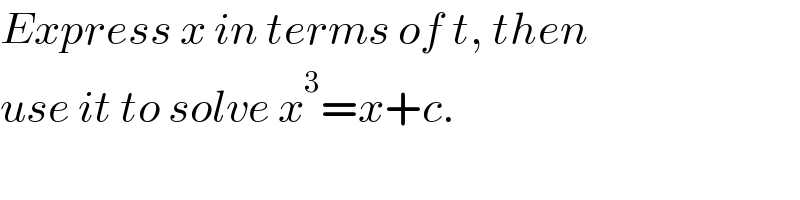
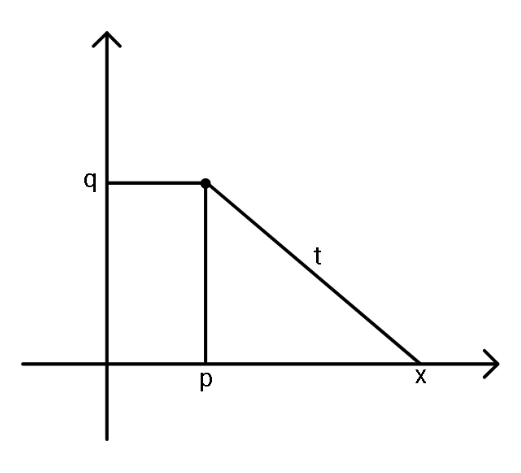
$${Express}\:{x}\:{in}\:{terms}\:{of}\:{t},\:{then} \\ $$$${use}\:{it}\:{to}\:{solve}\:{x}^{\mathrm{3}} ={x}+{c}. \\ $$
Answered by ajfour last updated on 09/Jan/21
![x=p+(√(t^2 −q^2 )) Now x^3 =x+c ⇒ p^3 +(t^2 −q^2 )(√(t^2 −q^2 )) +3p(t^2 −q^2 )+3p^2 (√(t^2 −q^2 )) −p−(√(t^2 −q^2 ))=c Let 3p^2 −q^2 =1 ⇒ p^3 +t^2 (√(t^2 +1−3p^2 ))+3p(t^2 +1−3p^2 ) −p−c=0 ⇒ [8p^3 −(2+3t^2 )p+c]^2 =t^4 (t^2 +1−3p^2 ) let t^2 =mp^2 +s ⇒ [8p^3 −2p−3p(mp^2 +s)+c]^2 = (mp^2 +s)^2 (mp^2 +s+1−3p^2 ) ⇒ let s=−1 ⇒ 8p^3 −2p−3p(mp^2 −1)+c =(√(m−3))(mp^2 −1)p ⇒ (8−3m−m(√(m−3)))p^3 +(1+(√(m−3)))p+c = 0 let (1+(√(m−3)))=r r^3 =1+(m−3)(√(m−3)) +3(√(m−3))+3(m−3) = −8+m(√(m−3))+3m .....](Q128649.png)
$${x}={p}+\sqrt{{t}^{\mathrm{2}} −{q}^{\mathrm{2}} } \\ $$$${Now}\:\:\:\:{x}^{\mathrm{3}} ={x}+{c}\:\:\:\Rightarrow \\ $$$${p}^{\mathrm{3}} +\left({t}^{\mathrm{2}} −{q}^{\mathrm{2}} \right)\sqrt{{t}^{\mathrm{2}} −{q}^{\mathrm{2}} } \\ $$$$+\mathrm{3}{p}\left({t}^{\mathrm{2}} −{q}^{\mathrm{2}} \right)+\mathrm{3}{p}^{\mathrm{2}} \sqrt{{t}^{\mathrm{2}} −{q}^{\mathrm{2}} } \\ $$$$−{p}−\sqrt{{t}^{\mathrm{2}} −{q}^{\mathrm{2}} }={c} \\ $$$$\:{Let}\:\:\:\:\mathrm{3}{p}^{\mathrm{2}} −{q}^{\mathrm{2}} =\mathrm{1}\:\:\:\:\Rightarrow \\ $$$${p}^{\mathrm{3}} +{t}^{\mathrm{2}} \sqrt{{t}^{\mathrm{2}} +\mathrm{1}−\mathrm{3}{p}^{\mathrm{2}} }+\mathrm{3}{p}\left({t}^{\mathrm{2}} +\mathrm{1}−\mathrm{3}{p}^{\mathrm{2}} \right) \\ $$$$−{p}−{c}=\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\:\left[\mathrm{8}{p}^{\mathrm{3}} −\left(\mathrm{2}+\mathrm{3}{t}^{\mathrm{2}} \right){p}+{c}\right]^{\mathrm{2}} ={t}^{\mathrm{4}} \left({t}^{\mathrm{2}} +\mathrm{1}−\mathrm{3}{p}^{\mathrm{2}} \right) \\ $$$${let}\:\:{t}^{\mathrm{2}} ={mp}^{\mathrm{2}} +{s} \\ $$$$\Rightarrow\:\left[\mathrm{8}{p}^{\mathrm{3}} −\mathrm{2}{p}−\mathrm{3}{p}\left({mp}^{\mathrm{2}} +{s}\right)+{c}\right]^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:=\:\left({mp}^{\mathrm{2}} +{s}\right)^{\mathrm{2}} \left({mp}^{\mathrm{2}} +{s}+\mathrm{1}−\mathrm{3}{p}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\:\:{let}\:\:\:{s}=−\mathrm{1} \\ $$$$\Rightarrow\:\:\mathrm{8}{p}^{\mathrm{3}} −\mathrm{2}{p}−\mathrm{3}{p}\left({mp}^{\mathrm{2}} −\mathrm{1}\right)+{c} \\ $$$$\:\:\:\:\:\:\:=\sqrt{{m}−\mathrm{3}}\left({mp}^{\mathrm{2}} −\mathrm{1}\right){p} \\ $$$$\Rightarrow \\ $$$$\left(\mathrm{8}−\mathrm{3}{m}−{m}\sqrt{{m}−\mathrm{3}}\right){p}^{\mathrm{3}} \\ $$$$\:\:\:\:\:+\left(\mathrm{1}+\sqrt{{m}−\mathrm{3}}\right){p}+{c}\:=\:\mathrm{0} \\ $$$${let}\:\:\:\left(\mathrm{1}+\sqrt{{m}−\mathrm{3}}\right)={r} \\ $$$${r}^{\mathrm{3}} =\mathrm{1}+\left({m}−\mathrm{3}\right)\sqrt{{m}−\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:+\mathrm{3}\sqrt{{m}−\mathrm{3}}+\mathrm{3}\left({m}−\mathrm{3}\right) \\ $$$$\:\:=\:−\mathrm{8}+{m}\sqrt{{m}−\mathrm{3}}+\mathrm{3}{m} \\ $$$$..... \\ $$
