
Question Number 128611 by malwan last updated on 08/Jan/21
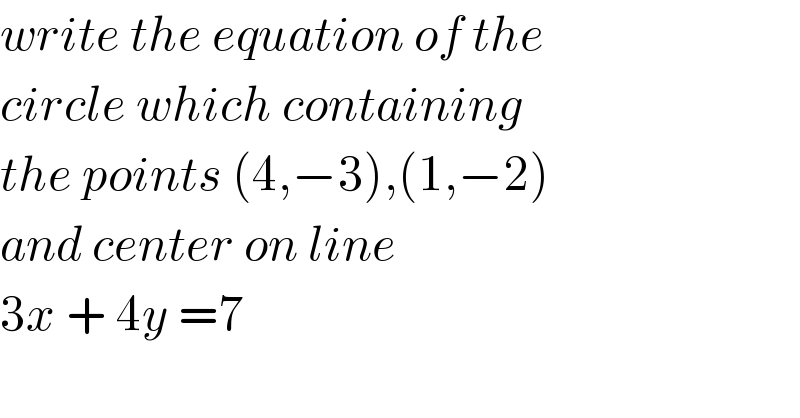
$${write}\:{the}\:{equation}\:{of}\:{the}\: \\ $$$${circle}\:{which}\:{containing}\: \\ $$$${the}\:{points}\:\left(\mathrm{4},−\mathrm{3}\right),\left(\mathrm{1},−\mathrm{2}\right) \\ $$$${and}\:{center}\:{on}\:{line} \\ $$$$\mathrm{3}{x}\:+\:\mathrm{4}{y}\:=\mathrm{7} \\ $$
Answered by mr W last updated on 09/Jan/21
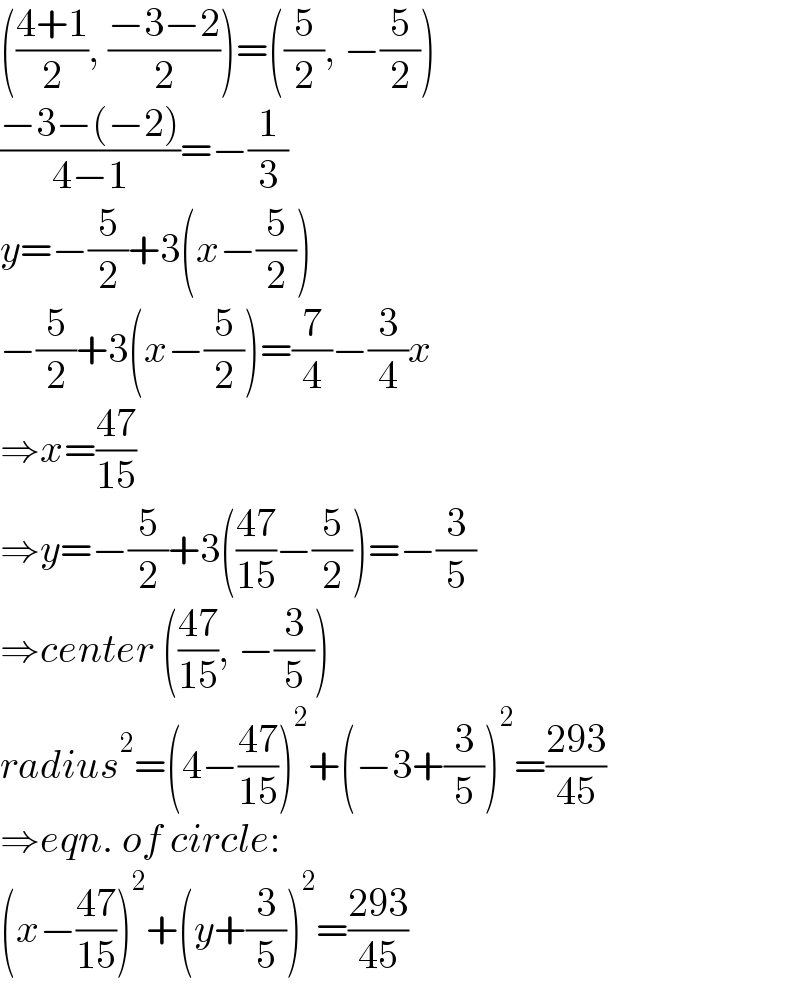
$$\left(\frac{\mathrm{4}+\mathrm{1}}{\mathrm{2}},\:\frac{−\mathrm{3}−\mathrm{2}}{\mathrm{2}}\right)=\left(\frac{\mathrm{5}}{\mathrm{2}},\:−\frac{\mathrm{5}}{\mathrm{2}}\right) \\ $$$$\frac{−\mathrm{3}−\left(−\mathrm{2}\right)}{\mathrm{4}−\mathrm{1}}=−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${y}=−\frac{\mathrm{5}}{\mathrm{2}}+\mathrm{3}\left({x}−\frac{\mathrm{5}}{\mathrm{2}}\right) \\ $$$$−\frac{\mathrm{5}}{\mathrm{2}}+\mathrm{3}\left({x}−\frac{\mathrm{5}}{\mathrm{2}}\right)=\frac{\mathrm{7}}{\mathrm{4}}−\frac{\mathrm{3}}{\mathrm{4}}{x} \\ $$$$\Rightarrow{x}=\frac{\mathrm{47}}{\mathrm{15}} \\ $$$$\Rightarrow{y}=−\frac{\mathrm{5}}{\mathrm{2}}+\mathrm{3}\left(\frac{\mathrm{47}}{\mathrm{15}}−\frac{\mathrm{5}}{\mathrm{2}}\right)=−\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$\Rightarrow{center}\:\left(\frac{\mathrm{47}}{\mathrm{15}},\:−\frac{\mathrm{3}}{\mathrm{5}}\right) \\ $$$${radius}^{\mathrm{2}} =\left(\mathrm{4}−\frac{\mathrm{47}}{\mathrm{15}}\right)^{\mathrm{2}} +\left(−\mathrm{3}+\frac{\mathrm{3}}{\mathrm{5}}\right)^{\mathrm{2}} =\frac{\mathrm{293}}{\mathrm{45}} \\ $$$$\Rightarrow{eqn}.\:{of}\:{circle}: \\ $$$$\left({x}−\frac{\mathrm{47}}{\mathrm{15}}\right)^{\mathrm{2}} +\left({y}+\frac{\mathrm{3}}{\mathrm{5}}\right)^{\mathrm{2}} =\frac{\mathrm{293}}{\mathrm{45}} \\ $$
Commented by malwan last updated on 09/Jan/21

$${thank}\:{you}\:{sir} \\ $$
Answered by liberty last updated on 08/Jan/21
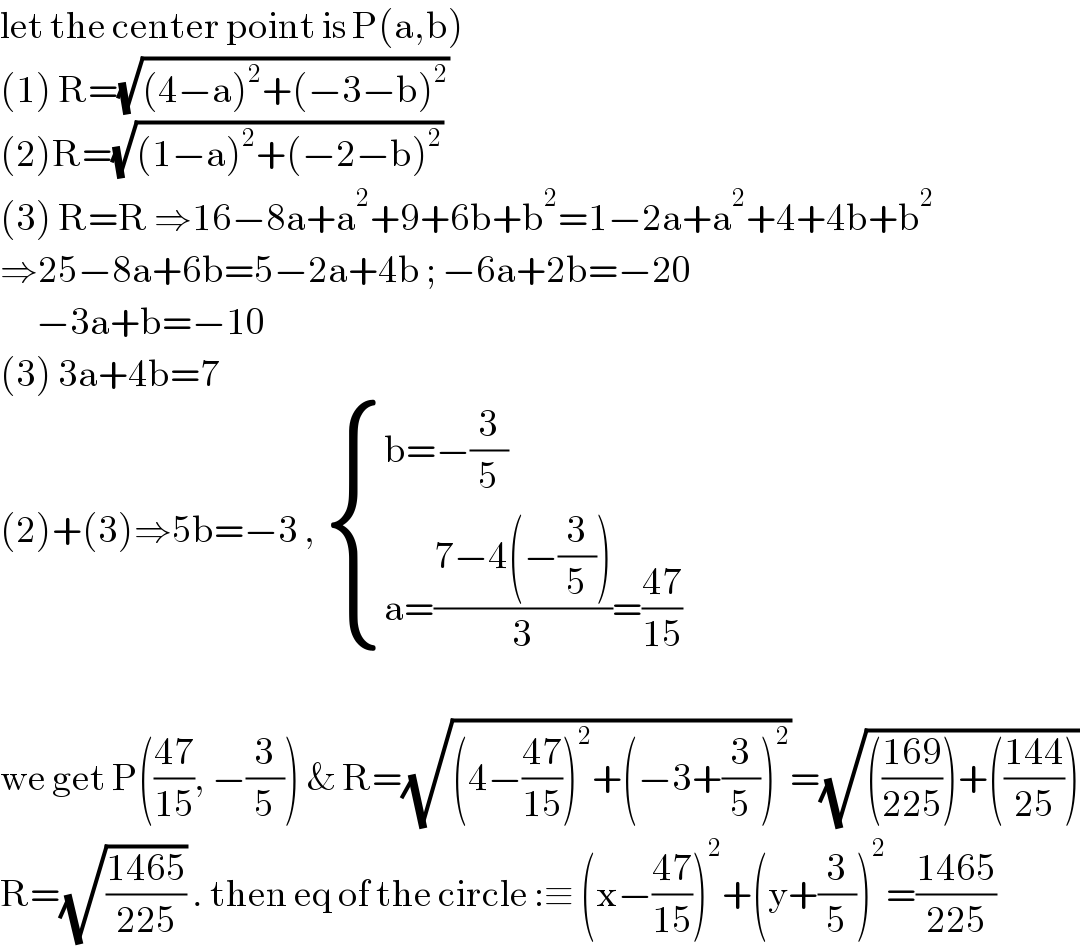
$$\mathrm{let}\:\mathrm{the}\:\mathrm{center}\:\mathrm{point}\:\mathrm{is}\:\mathrm{P}\left(\mathrm{a},\mathrm{b}\right)\: \\ $$$$\left(\mathrm{1}\right)\:\mathrm{R}=\sqrt{\left(\mathrm{4}−\mathrm{a}\right)^{\mathrm{2}} +\left(−\mathrm{3}−\mathrm{b}\right)^{\mathrm{2}} } \\ $$$$\left(\mathrm{2}\right)\mathrm{R}=\sqrt{\left(\mathrm{1}−\mathrm{a}\right)^{\mathrm{2}} +\left(−\mathrm{2}−\mathrm{b}\right)^{\mathrm{2}} } \\ $$$$\left(\mathrm{3}\right)\:\mathrm{R}=\mathrm{R}\:\Rightarrow\mathrm{16}−\mathrm{8a}+\mathrm{a}^{\mathrm{2}} +\mathrm{9}+\mathrm{6b}+\mathrm{b}^{\mathrm{2}} =\mathrm{1}−\mathrm{2a}+\mathrm{a}^{\mathrm{2}} +\mathrm{4}+\mathrm{4b}+\mathrm{b}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{25}−\mathrm{8a}+\mathrm{6b}=\mathrm{5}−\mathrm{2a}+\mathrm{4b}\:;\:−\mathrm{6a}+\mathrm{2b}=−\mathrm{20} \\ $$$$\:\:\:\:\:\:−\mathrm{3a}+\mathrm{b}=−\mathrm{10} \\ $$$$\left(\mathrm{3}\right)\:\mathrm{3a}+\mathrm{4b}=\mathrm{7}\: \\ $$$$\left(\mathrm{2}\right)+\left(\mathrm{3}\right)\Rightarrow\mathrm{5b}=−\mathrm{3}\:,\:\begin{cases}{\mathrm{b}=−\frac{\mathrm{3}}{\mathrm{5}}}\\{\mathrm{a}=\frac{\mathrm{7}−\mathrm{4}\left(−\frac{\mathrm{3}}{\mathrm{5}}\right)}{\mathrm{3}}=\frac{\mathrm{47}}{\mathrm{15}}}\end{cases} \\ $$$$ \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{P}\left(\frac{\mathrm{47}}{\mathrm{15}},\:−\frac{\mathrm{3}}{\mathrm{5}}\right)\:\&\:\mathrm{R}=\sqrt{\left(\mathrm{4}−\frac{\mathrm{47}}{\mathrm{15}}\right)^{\mathrm{2}} +\left(−\mathrm{3}+\frac{\mathrm{3}}{\mathrm{5}}\right)^{\mathrm{2}} }=\sqrt{\left(\frac{\mathrm{169}}{\mathrm{225}}\right)+\left(\frac{\mathrm{144}}{\mathrm{25}}\right)} \\ $$$$\mathrm{R}=\sqrt{\frac{\mathrm{1465}}{\mathrm{225}}}\:.\:\mathrm{then}\:\mathrm{eq}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circle}\::\equiv\:\left(\mathrm{x}−\frac{\mathrm{47}}{\mathrm{15}}\right)^{\mathrm{2}} +\left(\mathrm{y}+\frac{\mathrm{3}}{\mathrm{5}}\right)^{\mathrm{2}} =\frac{\mathrm{1465}}{\mathrm{225}} \\ $$
Commented by malwan last updated on 09/Jan/21
$${thank}\:{you}\:{so}\:{much} \\ $$
