
Question Number 128593 by Eric002 last updated on 08/Jan/21
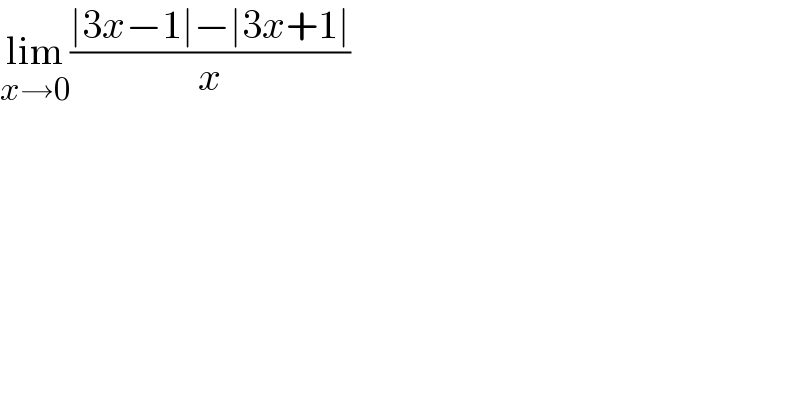
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mid\mathrm{3}{x}−\mathrm{1}\mid−\mid\mathrm{3}{x}+\mathrm{1}\mid}{{x}} \\ $$
Commented by MJS_new last updated on 08/Jan/21
![((∣3x−1∣−∣3x+1∣)/x)=(3/x)(∣x−(1/3)∣−∣x+(1/3)∣)= [−(1/3)≤x≤(1/3)] =(3/x)(−2x)=−((6x)/x)=−6∀x∈[−(1/3); (1/3)]∧x≠0 ⇒ limit is −6](Q128600.png)
$$\frac{\mid\mathrm{3}{x}−\mathrm{1}\mid−\mid\mathrm{3}{x}+\mathrm{1}\mid}{{x}}=\frac{\mathrm{3}}{{x}}\left(\mid{x}−\frac{\mathrm{1}}{\mathrm{3}}\mid−\mid{x}+\frac{\mathrm{1}}{\mathrm{3}}\mid\right)= \\ $$$$\:\:\:\:\:\left[−\frac{\mathrm{1}}{\mathrm{3}}\leqslant{x}\leqslant\frac{\mathrm{1}}{\mathrm{3}}\right] \\ $$$$=\frac{\mathrm{3}}{{x}}\left(−\mathrm{2}{x}\right)=−\frac{\mathrm{6}{x}}{{x}}=−\mathrm{6}\forall{x}\in\left[−\frac{\mathrm{1}}{\mathrm{3}};\:\frac{\mathrm{1}}{\mathrm{3}}\right]\wedge{x}\neq\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{limit}\:\mathrm{is}\:−\mathrm{6} \\ $$
Commented by john_santu last updated on 08/Jan/21
![lim_(x→0) (((√(9x^2 −6x+1))−(√(9x^2 +6x+1)))/x)= lim_(x→0) ((−12x)/(x[(√(9x^2 −6x+1))+(√(9x^2 +6x+1)) ]))= lim_(x→0) ((−12)/( (√(9x^2 −6x+1))+(√(9x^2 +6x+1))))=((−12)/2)=−6](Q128609.png)
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt{\mathrm{9x}^{\mathrm{2}} −\mathrm{6x}+\mathrm{1}}−\sqrt{\mathrm{9x}^{\mathrm{2}} +\mathrm{6x}+\mathrm{1}}}{\mathrm{x}}= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{−\mathrm{12x}}{\mathrm{x}\left[\sqrt{\mathrm{9x}^{\mathrm{2}} −\mathrm{6x}+\mathrm{1}}+\sqrt{\mathrm{9x}^{\mathrm{2}} +\mathrm{6x}+\mathrm{1}}\:\right]}= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{12}}{\:\sqrt{\mathrm{9x}^{\mathrm{2}} −\mathrm{6x}+\mathrm{1}}+\sqrt{\mathrm{9x}^{\mathrm{2}} +\mathrm{6x}+\mathrm{1}}}=\frac{−\mathrm{12}}{\mathrm{2}}=−\mathrm{6} \\ $$
Answered by Olaf last updated on 08/Jan/21
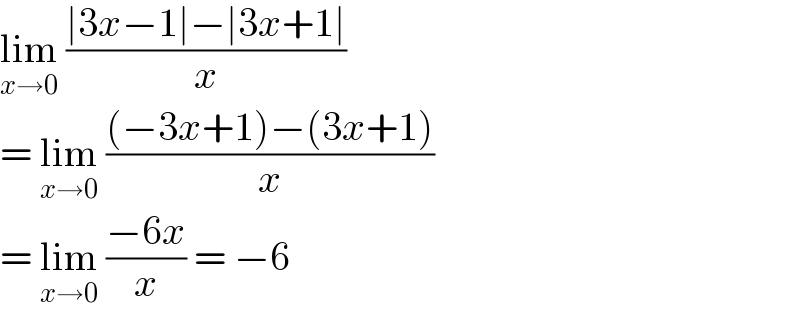
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mid\mathrm{3}{x}−\mathrm{1}\mid−\mid\mathrm{3}{x}+\mathrm{1}\mid}{{x}} \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(−\mathrm{3}{x}+\mathrm{1}\right)−\left(\mathrm{3}{x}+\mathrm{1}\right)}{{x}} \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{6}{x}}{{x}}\:=\:−\mathrm{6} \\ $$
