
Question Number 128590 by I want to learn more last updated on 08/Jan/21
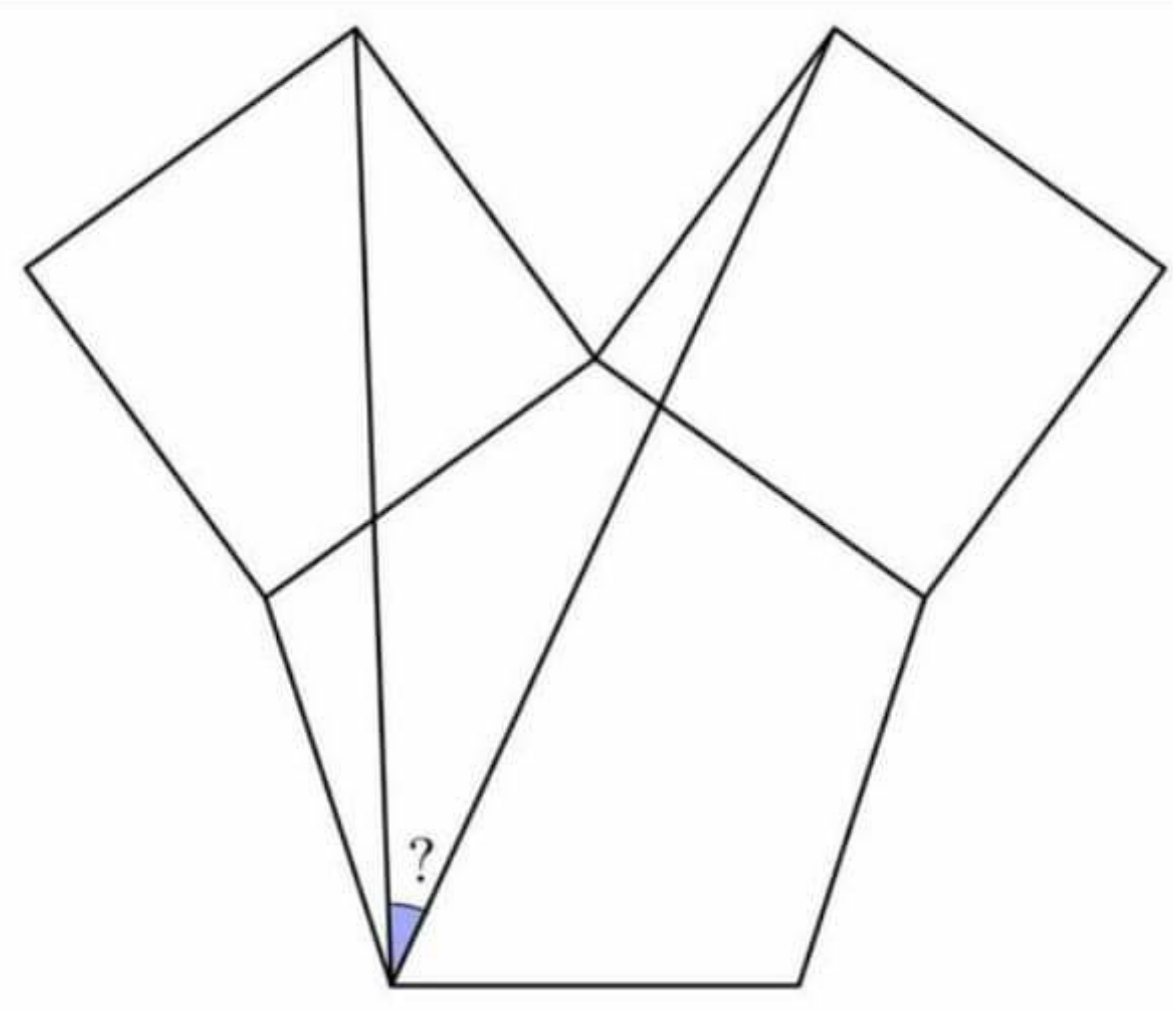
Answered by mr W last updated on 08/Jan/21
Commented by mr W last updated on 08/Jan/21

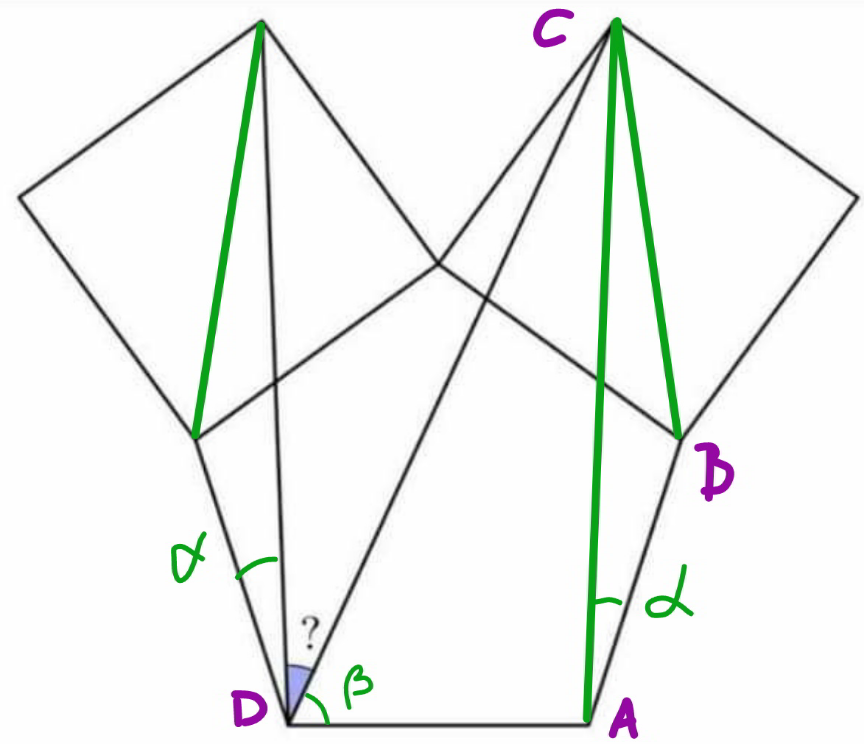
$${AB}=\mathrm{1} \\ $$$${BC}=\sqrt{\mathrm{2}} \\ $$$$\frac{\mathrm{3}×\mathrm{180}°}{\mathrm{5}}=\mathrm{108}° \\ $$$${AC}=\sqrt{\mathrm{1}^{\mathrm{2}} +\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{2}×\mathrm{1}×\sqrt{\mathrm{2}}×\mathrm{cos}\:\left(\mathrm{108}+\mathrm{45}\right)} \\ $$$$=\sqrt{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\mathrm{cos}\:\mathrm{27}°} \\ $$$$\frac{\mathrm{sin}\:\alpha}{\:\sqrt{\mathrm{2}}}=\frac{\mathrm{sin}\:\left(\mathrm{108}+\mathrm{45}\right)}{\:\sqrt{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\mathrm{cos}\:\mathrm{27}}} \\ $$$$\Rightarrow\mathrm{sin}\:\alpha=\frac{\sqrt{\mathrm{2}}\mathrm{sin}\:\left(\mathrm{27}\right)}{\:\sqrt{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\mathrm{cos}\:\mathrm{27}}} \\ $$$$\frac{\mathrm{sin}\:\left(\beta+\mathrm{108}−\alpha\right)}{\mathrm{1}}=\frac{\mathrm{sin}\:\beta}{\:\sqrt{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\mathrm{cos}\:\mathrm{27}}} \\ $$$$\frac{\mathrm{sin}\:\beta\:\mathrm{cos}\:\left(\mathrm{108}−\alpha\right)+\mathrm{cos}\:\beta\:\mathrm{sin}\:\left(\mathrm{108}−\alpha\right)}{\mathrm{sin}\:\beta}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\mathrm{cos}\:\mathrm{27}}} \\ $$$$−\mathrm{sin}\:\left(\mathrm{18}−\alpha\right)+\frac{\mathrm{cos}\:\left(\mathrm{18}−\alpha\right)}{\mathrm{tan}\:\beta}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\mathrm{cos}\:\mathrm{27}}} \\ $$$$\Rightarrow\mathrm{tan}\:\beta=\frac{\mathrm{cos}\:\left(\mathrm{18}−\alpha\right)}{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\mathrm{cos}\:\mathrm{27}}}+\mathrm{sin}\:\left(\mathrm{18}−\alpha\right)} \\ $$$$\Rightarrow\alpha=\mathrm{15}.\mathrm{858737}° \\ $$$$\Rightarrow\beta=\mathrm{65}.\mathrm{141263}° \\ $$$$\Rightarrow?=\mathrm{108}−\alpha−\beta=\mathrm{27}° \\ $$
Commented by I want to learn more last updated on 08/Jan/21
$$\mathrm{Thanks}\:\mathrm{sir},\:\:\mathrm{i}\:\mathrm{appreciate}. \\ $$
Answered by mr W last updated on 08/Jan/21
Commented by mr W last updated on 08/Jan/21

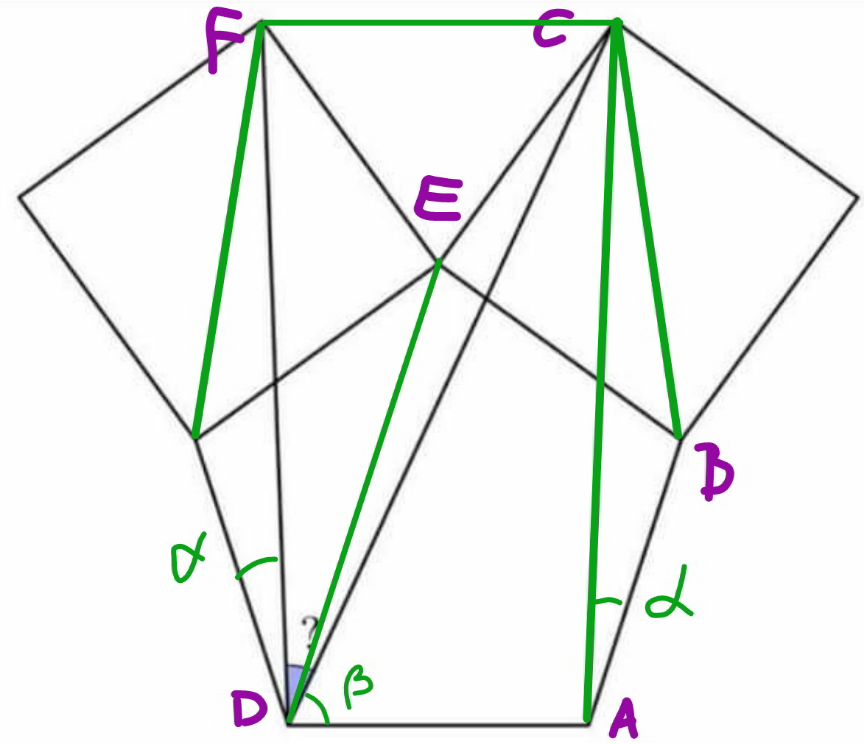
$${DE}=\mathrm{2}×\mathrm{1}×\mathrm{sin}\:\frac{\mathrm{108}}{\mathrm{2}}=\mathrm{2}\:\mathrm{sin}\:\mathrm{54}° \\ $$$${FC}=\mathrm{2}×\mathrm{1}×\mathrm{sin}\:\frac{\mathrm{180}−\mathrm{108}}{\mathrm{2}}=\mathrm{2}\:\mathrm{sin}\:\mathrm{36}° \\ $$$$\angle{CFD}=\mathrm{90}+\mathrm{108}−\frac{\mathrm{180}−\mathrm{108}}{\mathrm{2}}=\mathrm{162}° \\ $$$${DC}^{\mathrm{2}} =\mathrm{1}^{\mathrm{2}} +\left(\mathrm{2}\:\mathrm{sin}\:\mathrm{54}\right)^{\mathrm{2}} −\mathrm{2}×\mathrm{1}×\mathrm{2}×\mathrm{sin}\:\mathrm{54}×\mathrm{cos}\:\mathrm{162} \\ $$$$=\mathrm{1}+\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{54}+\mathrm{4}\:\mathrm{sin}\:\mathrm{54}\:\mathrm{cos}\:\mathrm{18} \\ $$$${DF}^{\mathrm{2}} =\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\:\mathrm{cos}\:\mathrm{27} \\ $$$$\left(\mathrm{2}\:\mathrm{sin}\:\mathrm{36}\right)^{\mathrm{2}} =\mathrm{1}+\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{54}+\mathrm{4}\:\mathrm{sin}\:\mathrm{54}\:\mathrm{cos}\:\mathrm{18}+\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\:\mathrm{cos}\:\mathrm{27}−\mathrm{2}\:\mathrm{cos}\:{x}\:\sqrt{\left(\mathrm{1}+\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{54}+\mathrm{4}\:\mathrm{sin}\:\mathrm{54}\:\mathrm{cos}\:\mathrm{18}\right)\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\:\mathrm{cos}\:\mathrm{27}\right)} \\ $$$$\mathrm{cos}\:{x}=\frac{\mathrm{2}+\mathrm{2}\:\mathrm{sin}\:\mathrm{54}\:\mathrm{cos}\:\mathrm{18}+\sqrt{\mathrm{2}}\:\mathrm{cos}\:\mathrm{27}−\mathrm{2}\:\mathrm{sin}\:\mathrm{18}}{\:\sqrt{\left(\mathrm{1}+\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{54}+\mathrm{4}\:\mathrm{sin}\:\mathrm{54}\:\mathrm{cos}\:\mathrm{18}\right)\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\:\mathrm{cos}\:\mathrm{27}\right)}} \\ $$$$... \\ $$
Commented by I want to learn more last updated on 08/Jan/21

$$\mathrm{Thanks}\:\mathrm{sir},\:\:\mathrm{i}\:\mathrm{appreciate} \\ $$
