
Question Number 128575 by Study last updated on 08/Jan/21
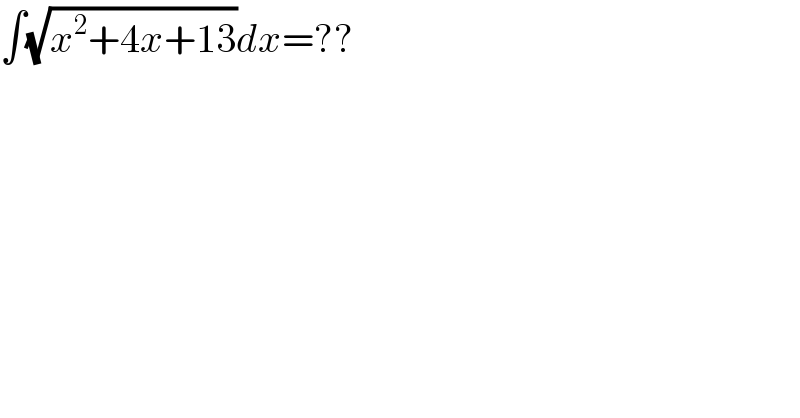
$$\int\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{13}}{dx}=?? \\ $$
Commented by MJS_new last updated on 08/Jan/21
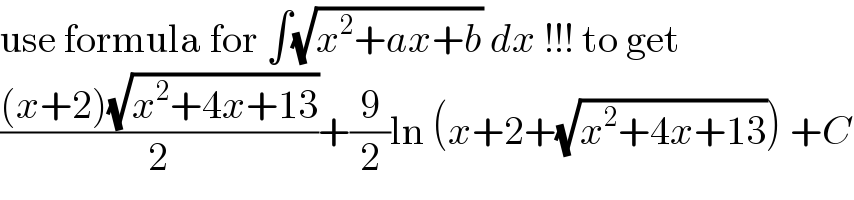
$$\mathrm{use}\:\mathrm{formula}\:\mathrm{for}\:\int\sqrt{{x}^{\mathrm{2}} +{ax}+{b}}\:{dx}\:!!!\:\mathrm{to}\:\mathrm{get} \\ $$$$\frac{\left({x}+\mathrm{2}\right)\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{13}}}{\mathrm{2}}+\frac{\mathrm{9}}{\mathrm{2}}\mathrm{ln}\:\left({x}+\mathrm{2}+\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{13}}\right)\:+{C} \\ $$
Commented by Study last updated on 08/Jan/21

$${which}\:{formula}? \\ $$
Commented by MJS_new last updated on 08/Jan/21

$$\mathrm{you}\:\mathrm{could}\:\mathrm{search}\:\mathrm{the}\:\mathrm{web}\:\mathrm{for}\:\mathrm{integration} \\ $$$$\mathrm{formulas},\:\mathrm{couldn}'\mathrm{t}\:\mathrm{you}? \\ $$
Answered by john_santu last updated on 08/Jan/21
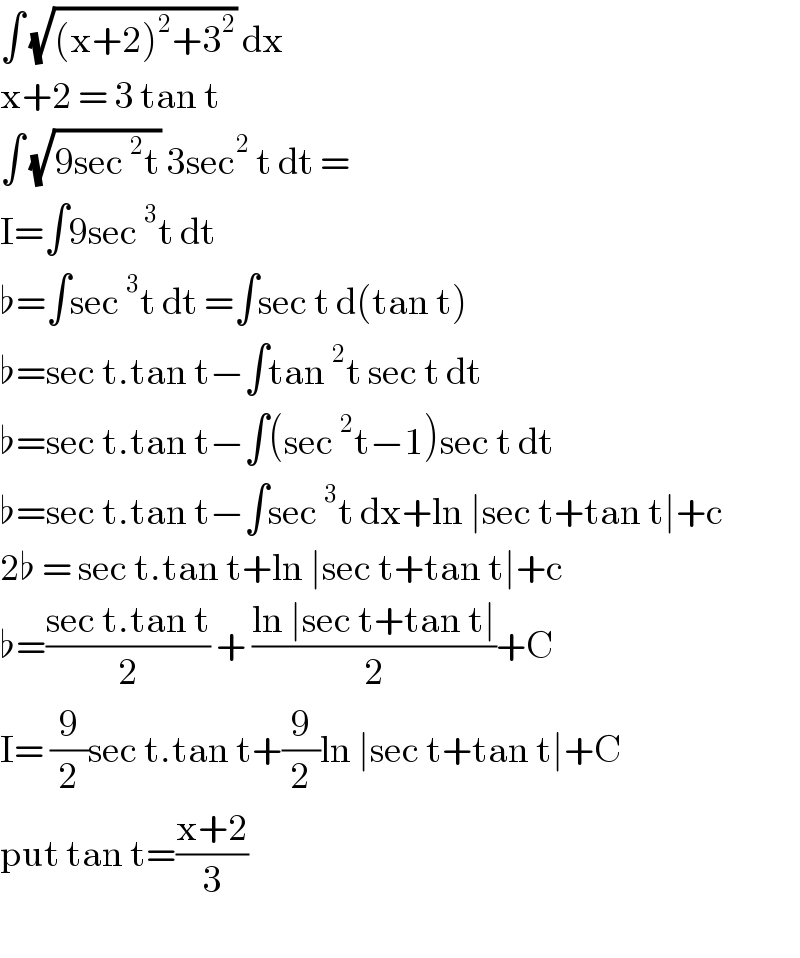
$$\int\:\sqrt{\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} }\:\mathrm{dx}\: \\ $$$$\mathrm{x}+\mathrm{2}\:=\:\mathrm{3}\:\mathrm{tan}\:\mathrm{t} \\ $$$$\int\:\sqrt{\mathrm{9sec}\:^{\mathrm{2}} \mathrm{t}}\:\mathrm{3sec}^{\mathrm{2}} \:\mathrm{t}\:\mathrm{dt}\:= \\ $$$$\mathrm{I}=\int\mathrm{9sec}\:^{\mathrm{3}} \mathrm{t}\:\mathrm{dt}\: \\ $$$$\flat=\int\mathrm{sec}\:^{\mathrm{3}} \mathrm{t}\:\mathrm{dt}\:=\int\mathrm{sec}\:\mathrm{t}\:\mathrm{d}\left(\mathrm{tan}\:\mathrm{t}\right) \\ $$$$\flat=\mathrm{sec}\:\mathrm{t}.\mathrm{tan}\:\mathrm{t}−\int\mathrm{tan}\:^{\mathrm{2}} \mathrm{t}\:\mathrm{sec}\:\mathrm{t}\:\mathrm{dt} \\ $$$$\flat=\mathrm{sec}\:\mathrm{t}.\mathrm{tan}\:\mathrm{t}−\int\left(\mathrm{sec}\:^{\mathrm{2}} \mathrm{t}−\mathrm{1}\right)\mathrm{sec}\:\mathrm{t}\:\mathrm{dt} \\ $$$$\flat=\mathrm{sec}\:\mathrm{t}.\mathrm{tan}\:\mathrm{t}−\int\mathrm{sec}\:^{\mathrm{3}} \mathrm{t}\:\mathrm{dx}+\mathrm{ln}\:\mid\mathrm{sec}\:\mathrm{t}+\mathrm{tan}\:\mathrm{t}\mid+\mathrm{c} \\ $$$$\mathrm{2}\flat\:=\:\mathrm{sec}\:\mathrm{t}.\mathrm{tan}\:\mathrm{t}+\mathrm{ln}\:\mid\mathrm{sec}\:\mathrm{t}+\mathrm{tan}\:\mathrm{t}\mid+\mathrm{c} \\ $$$$\flat=\frac{\mathrm{sec}\:\mathrm{t}.\mathrm{tan}\:\mathrm{t}}{\mathrm{2}}\:+\:\frac{\mathrm{ln}\:\mid\mathrm{sec}\:\mathrm{t}+\mathrm{tan}\:\mathrm{t}\mid}{\mathrm{2}}+\mathrm{C} \\ $$$$\mathrm{I}=\:\frac{\mathrm{9}}{\mathrm{2}}\mathrm{sec}\:\mathrm{t}.\mathrm{tan}\:\mathrm{t}+\frac{\mathrm{9}}{\mathrm{2}}\mathrm{ln}\:\mid\mathrm{sec}\:\mathrm{t}+\mathrm{tan}\:\mathrm{t}\mid+\mathrm{C}\: \\ $$$$\mathrm{put}\:\mathrm{tan}\:\mathrm{t}=\frac{\mathrm{x}+\mathrm{2}}{\mathrm{3}} \\ $$$$ \\ $$
Answered by MJS_new last updated on 08/Jan/21
![sometimes you seem like a kid with a bicycle asking how to drive a racing car through a chicane... ∫(√(x^2 +4x+13)) dx=∫(√((x+2)^2 +9)) dx= [t=x+2 ⇔ x=t−2 → dx=dt] =∫(√(t^2 +9)) dt= [u=((t+(√(t^2 +9)))/3) ⇔ t=((3(u^2 −1))/2) → dt=((3(√(t^2 +9)) du)/(t+(√(t^2 +9))))] =(9/4)∫(((u^2 +1)^2 )/u^3 )du=(9/4)∫u+(2/u)+(1/u^3 ) du and I hope you can go on from here](Q128580.png)
$$\mathrm{sometimes}\:\mathrm{you}\:\mathrm{seem}\:\mathrm{like}\:\mathrm{a}\:\mathrm{kid}\:\mathrm{with}\:\mathrm{a}\:\mathrm{bicycle} \\ $$$$\mathrm{asking}\:\mathrm{how}\:\mathrm{to}\:\mathrm{drive}\:\mathrm{a}\:\mathrm{racing}\:\mathrm{car}\:\mathrm{through}\:\mathrm{a} \\ $$$$\mathrm{chicane}... \\ $$$$\int\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{13}}\:{dx}=\int\sqrt{\left({x}+\mathrm{2}\right)^{\mathrm{2}} +\mathrm{9}}\:{dx}= \\ $$$$\:\:\:\:\:\left[{t}={x}+\mathrm{2}\:\Leftrightarrow\:{x}={t}−\mathrm{2}\:\rightarrow\:{dx}={dt}\right] \\ $$$$=\int\sqrt{{t}^{\mathrm{2}} +\mathrm{9}}\:{dt}= \\ $$$$\:\:\:\:\:\left[{u}=\frac{{t}+\sqrt{{t}^{\mathrm{2}} +\mathrm{9}}}{\mathrm{3}}\:\Leftrightarrow\:\:{t}=\frac{\mathrm{3}\left({u}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{2}}\:\rightarrow\:{dt}=\frac{\mathrm{3}\sqrt{{t}^{\mathrm{2}} +\mathrm{9}}\:{du}}{{t}+\sqrt{{t}^{\mathrm{2}} +\mathrm{9}}}\right] \\ $$$$=\frac{\mathrm{9}}{\mathrm{4}}\int\frac{\left({u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{{u}^{\mathrm{3}} }{du}=\frac{\mathrm{9}}{\mathrm{4}}\int{u}+\frac{\mathrm{2}}{{u}}+\frac{\mathrm{1}}{{u}^{\mathrm{3}} }\:{du} \\ $$$$\mathrm{and}\:\mathrm{I}\:\mathrm{hope}\:\mathrm{you}\:\mathrm{can}\:\mathrm{go}\:\mathrm{on}\:\mathrm{from}\:\mathrm{here} \\ $$
Commented by john_santu last updated on 08/Jan/21
��������������������������
Answered by Dwaipayan Shikari last updated on 08/Jan/21
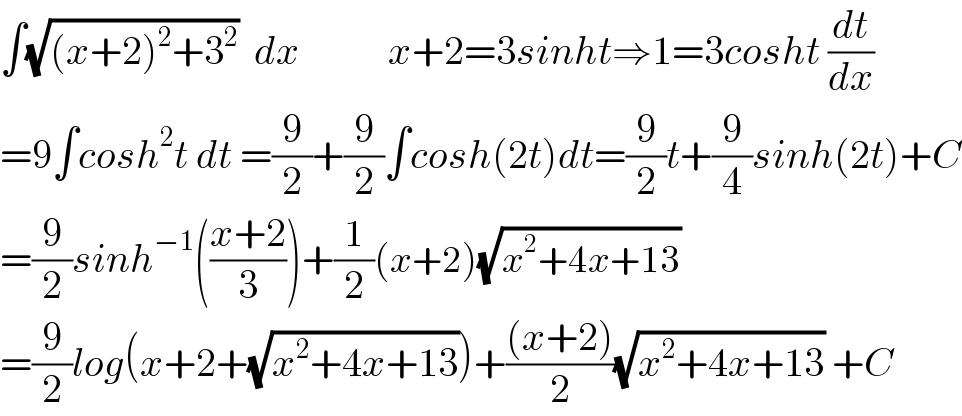
$$\int\sqrt{\left({x}+\mathrm{2}\right)^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} }\:\:{dx}\:\:\:\:\:\:\:\:\:\:\:{x}+\mathrm{2}=\mathrm{3}{sinht}\Rightarrow\mathrm{1}=\mathrm{3}{cosht}\:\frac{{dt}}{{dx}} \\ $$$$=\mathrm{9}\int{cosh}^{\mathrm{2}} {t}\:{dt}\:=\frac{\mathrm{9}}{\mathrm{2}}+\frac{\mathrm{9}}{\mathrm{2}}\int{cosh}\left(\mathrm{2}{t}\right){dt}=\frac{\mathrm{9}}{\mathrm{2}}{t}+\frac{\mathrm{9}}{\mathrm{4}}{sinh}\left(\mathrm{2}{t}\right)+{C} \\ $$$$=\frac{\mathrm{9}}{\mathrm{2}}{sinh}^{−\mathrm{1}} \left(\frac{{x}+\mathrm{2}}{\mathrm{3}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\left({x}+\mathrm{2}\right)\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{13}} \\ $$$$=\frac{\mathrm{9}}{\mathrm{2}}{log}\left({x}+\mathrm{2}+\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{13}}\right)+\frac{\left({x}+\mathrm{2}\right)}{\mathrm{2}}\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{13}}\:+{C} \\ $$
