
Question Number 128529 by bramlexs22 last updated on 08/Jan/21
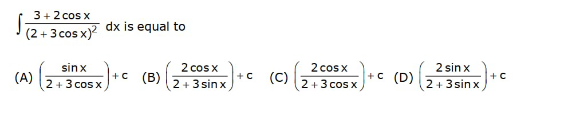
Commented by liberty last updated on 08/Jan/21
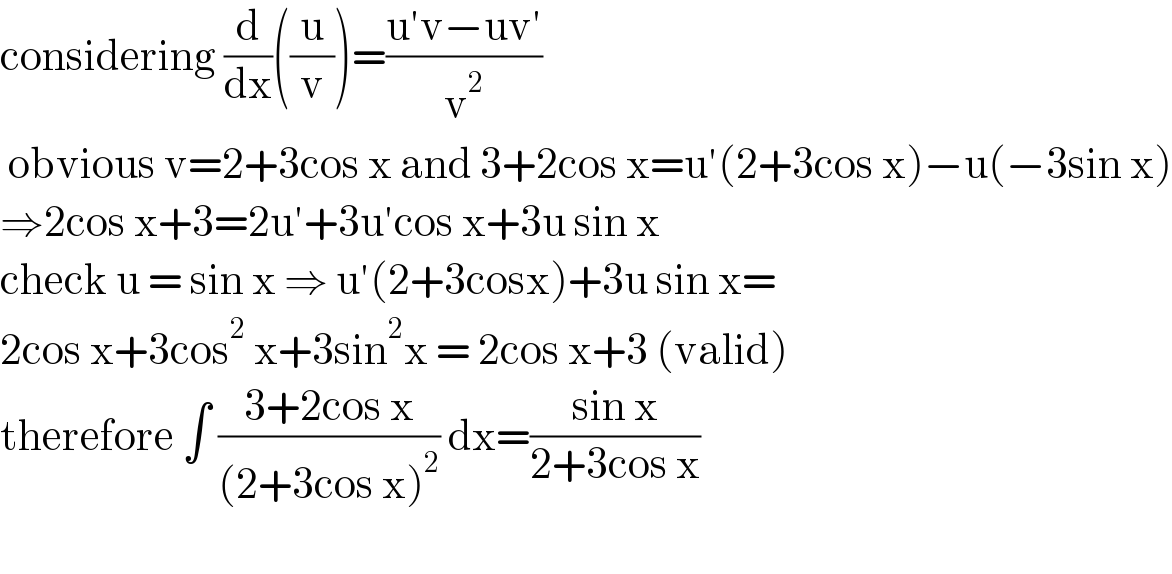
$$\mathrm{considering}\:\frac{\mathrm{d}}{\mathrm{dx}}\left(\frac{\mathrm{u}}{\mathrm{v}}\right)=\frac{\mathrm{u}'\mathrm{v}−\mathrm{uv}'}{\mathrm{v}^{\mathrm{2}} } \\ $$$$\:\mathrm{obvious}\:\mathrm{v}=\mathrm{2}+\mathrm{3cos}\:\mathrm{x}\:\mathrm{and}\:\mathrm{3}+\mathrm{2cos}\:\mathrm{x}=\mathrm{u}'\left(\mathrm{2}+\mathrm{3cos}\:\mathrm{x}\right)−\mathrm{u}\left(−\mathrm{3sin}\:\mathrm{x}\right) \\ $$$$\Rightarrow\mathrm{2cos}\:\mathrm{x}+\mathrm{3}=\mathrm{2u}'+\mathrm{3u}'\mathrm{cos}\:\mathrm{x}+\mathrm{3u}\:\mathrm{sin}\:\mathrm{x} \\ $$$$\mathrm{check}\:\mathrm{u}\:=\:\mathrm{sin}\:\mathrm{x}\:\Rightarrow\:\mathrm{u}'\left(\mathrm{2}+\mathrm{3cosx}\right)+\mathrm{3u}\:\mathrm{sin}\:\mathrm{x}=\: \\ $$$$\mathrm{2cos}\:\mathrm{x}+\mathrm{3cos}^{\mathrm{2}} \:\mathrm{x}+\mathrm{3sin}^{\mathrm{2}} \mathrm{x}\:=\:\mathrm{2cos}\:\mathrm{x}+\mathrm{3}\:\left(\mathrm{valid}\right)\:\: \\ $$$$\mathrm{therefore}\:\int\:\frac{\mathrm{3}+\mathrm{2cos}\:\mathrm{x}}{\left(\mathrm{2}+\mathrm{3cos}\:\mathrm{x}\right)^{\mathrm{2}} }\:\mathrm{dx}=\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{2}+\mathrm{3cos}\:\mathrm{x}}\: \\ $$$$ \\ $$
Commented by SLVR last updated on 08/Jan/21
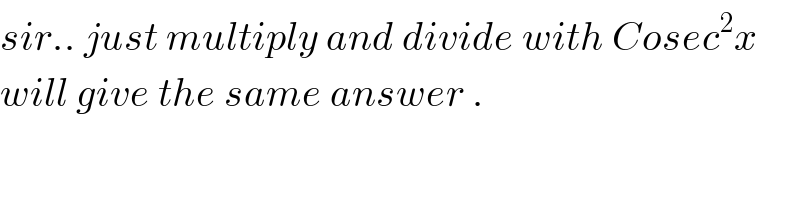
$${sir}..\:{just}\:{multiply}\:{and}\:{divide}\:{with}\:{Cosec}^{\mathrm{2}} {x}\: \\ $$$${will}\:{give}\:{the}\:{same}\:{answer}\:. \\ $$
Answered by SLVR last updated on 08/Jan/21

$$ \\ $$
Commented by bramlexs22 last updated on 08/Jan/21

$$\mathrm{what}\:? \\ $$
Commented by SLVR last updated on 08/Jan/21
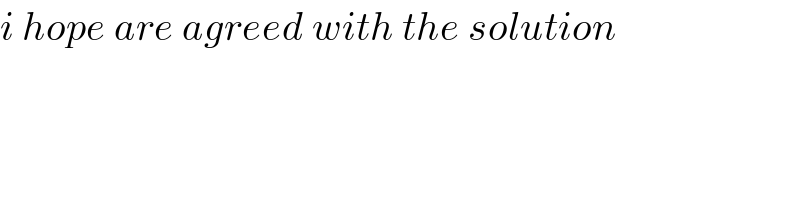
$${i}\:{hope}\:{are}\:{agreed}\:{with}\:{the}\:{solution} \\ $$
Commented by john_santu last updated on 08/Jan/21
$$\mathrm{what}\:\mathrm{your}\:\mathrm{solution}? \\ $$
Commented by SLVR last updated on 09/Jan/21
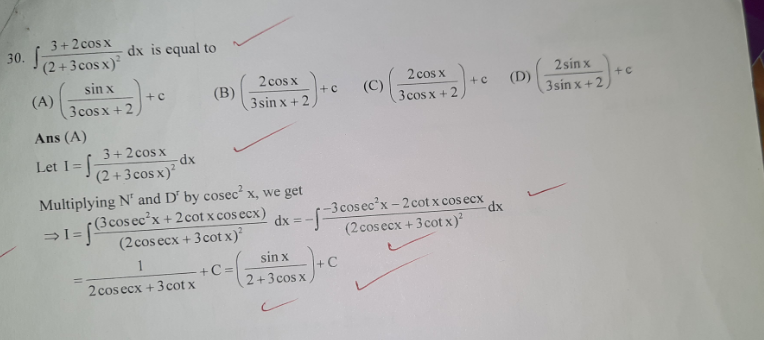
Commented by SLVR last updated on 09/Jan/21

$${sorry}...\:{i}\:{didnot}\:{observed}\:{uploading}\:{part} \\ $$
