
Question Number 128511 by benjo_mathlover last updated on 08/Jan/21
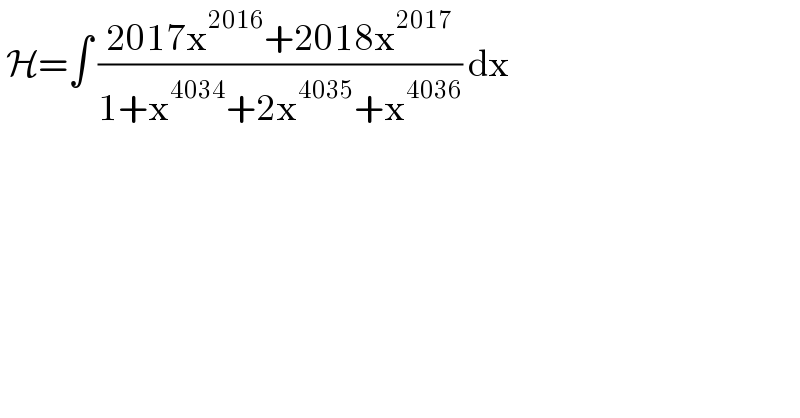
$$\:\mathcal{H}=\int\:\frac{\mathrm{2017x}^{\mathrm{2016}} +\mathrm{2018x}^{\mathrm{2017}} }{\mathrm{1}+\mathrm{x}^{\mathrm{4034}} +\mathrm{2x}^{\mathrm{4035}} +\mathrm{x}^{\mathrm{4036}} }\:\mathrm{dx}\: \\ $$
Answered by liberty last updated on 08/Jan/21
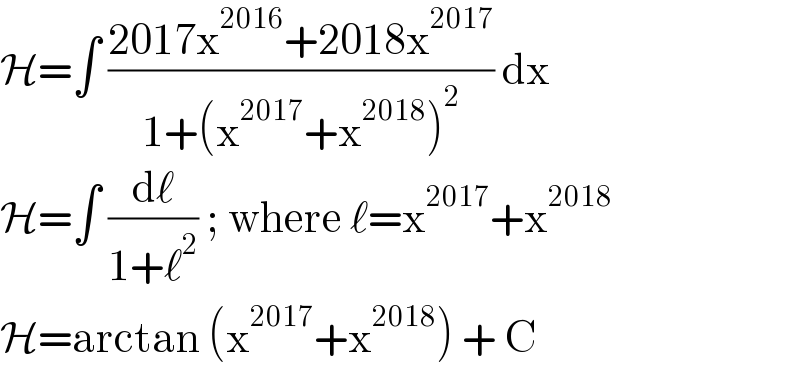
$$\mathcal{H}=\int\:\frac{\mathrm{2017x}^{\mathrm{2016}} +\mathrm{2018x}^{\mathrm{2017}} }{\mathrm{1}+\left(\mathrm{x}^{\mathrm{2017}} +\mathrm{x}^{\mathrm{2018}} \right)^{\mathrm{2}} }\:\mathrm{dx} \\ $$$$\mathcal{H}=\int\:\frac{\mathrm{d}\ell}{\mathrm{1}+\ell^{\mathrm{2}} }\:;\:\mathrm{where}\:\ell=\mathrm{x}^{\mathrm{2017}} +\mathrm{x}^{\mathrm{2018}} \\ $$$$\mathcal{H}=\mathrm{arctan}\:\left(\mathrm{x}^{\mathrm{2017}} +\mathrm{x}^{\mathrm{2018}} \right)\:+\:\mathrm{C} \\ $$
Commented by bramlexs22 last updated on 08/Jan/21

$$\mathrm{waw}.... \\ $$
