
Question Number 128462 by Ari last updated on 07/Jan/21
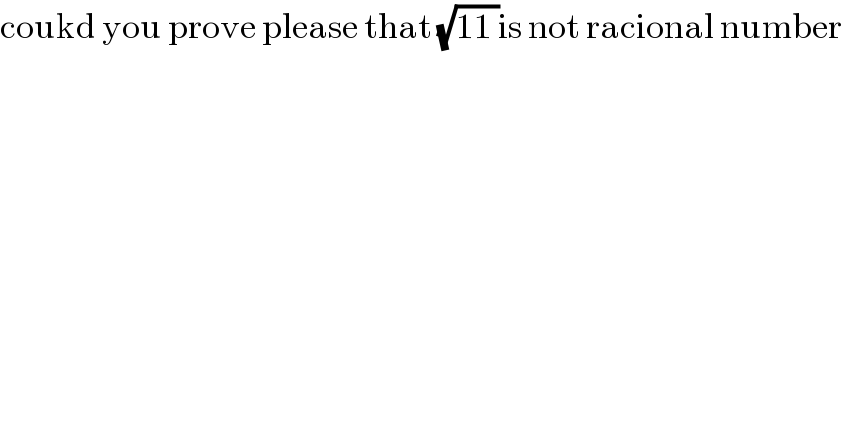
$$\mathrm{coukd}\:\mathrm{you}\:\mathrm{prove}\:\mathrm{please}\:\mathrm{that}\:\sqrt{\mathrm{11}\:}\mathrm{is}\:\mathrm{not}\:\mathrm{racional}\:\mathrm{number} \\ $$
Answered by Dwaipayan Shikari last updated on 07/Jan/21

$$\sqrt{\mathrm{11}}=\mathrm{3}+\sqrt{\mathrm{11}}−\mathrm{3}=\mathrm{3}+\frac{\mathrm{2}}{\:\sqrt{\mathrm{11}}+\mathrm{3}}=\mathrm{3}+\frac{\mathrm{2}}{\mathrm{3}+\mathrm{3}+\frac{\mathrm{2}}{\mathrm{3}+\mathrm{3}+\frac{\mathrm{2}}{\mathrm{3}+\mathrm{3}+\frac{\mathrm{2}}{\mathrm{3}+\mathrm{3}...}}}} \\ $$$$=\mathrm{3}+\frac{\mathrm{2}}{\mathrm{6}+\frac{\mathrm{2}}{\mathrm{6}+\frac{\mathrm{2}}{\mathrm{6}+\frac{\mathrm{2}}{\mathrm{6}+\frac{\mathrm{2}}{\mathrm{6}+...}}}}}\:\:\:\:\: \\ $$$${It}\:{is}\:{an}\:{Infinte}\:{continued}\:{fraction}\:.{So}\:{it}\:{can}\:{never}\:{be}\:{Rational} \\ $$$${Or} \\ $$$$\sqrt{\mathrm{11}}=\mathrm{1}+\frac{\mathrm{10}}{\:\sqrt{\mathrm{11}}+\mathrm{1}}=\mathrm{1}+\frac{\mathrm{10}}{\mathrm{2}+\frac{\mathrm{10}}{\mathrm{2}+\frac{\mathrm{10}}{\mathrm{2}+\frac{\mathrm{10}}{\mathrm{2}+...}}}} \\ $$
Commented by Ari last updated on 07/Jan/21
Yes,one way !
Answered by physicstutes last updated on 07/Jan/21

$$\mathrm{let}'\mathrm{s}\:\mathrm{do}\:\mathrm{it}\:\mathrm{by}\:\mathrm{contradiction}. \\ $$$$\:\mathrm{let}'\mathrm{s}\:\mathrm{assume}\:\mathrm{that}\:\sqrt{\mathrm{11}}\:\mathrm{was}\:\mathrm{rational}. \\ $$$$\mathrm{then}\:\:\sqrt{\mathrm{11}}\:=\:\frac{{a}}{{b}}\:\mathrm{where}\:{a}\:\mathrm{and}\:{b}\:\mathrm{are}\:\mathrm{in}\:\mathrm{thier}\:\mathrm{simpliest}\:\mathrm{term}. \\ $$$$\Rightarrow\:\mathrm{11}\:=\:\left(\frac{{a}}{{b}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:{a}^{\mathrm{2}} \:=\:\mathrm{11}{b}^{\mathrm{2}} \:\:\mathrm{so}\:\mathrm{we}\:\mathrm{can}\:\mathrm{say}\:{a}\:=\:\mathrm{11}{k}\:\left(\mathrm{an}\:\mathrm{assumption}\right) \\ $$$$\Rightarrow\:{a}^{\mathrm{2}} \:=\:\mathrm{11}^{\mathrm{2}} {k}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\mathrm{11}{b}^{\mathrm{2}} \:=\:\mathrm{11}^{\mathrm{2}} {k}^{\mathrm{2}} \:\mathrm{hence}\:{b}^{\mathrm{2}} \:=\:\mathrm{11}\:{k}^{\mathrm{2}} \:\mathrm{so}\:{b}\:=\:\mathrm{11}{m} \\ $$$$\mathrm{thus}\:\mathrm{gcd}\left({a},{b}\right)\:=\:\mathrm{11}\:\mathrm{which}\:\mathrm{contradicts}\:\mathrm{that}\:\mathrm{fact}\:\mathrm{that}\:\mathrm{gcd}\left({a},{b}\right)\:=\:\mathrm{1} \\ $$$$\mathrm{hence}\:\sqrt{\mathrm{11}}\:\mathrm{is}\:\mathrm{not}\:\mathrm{rational}. \\ $$
Commented by Ari last updated on 07/Jan/21
Yes,you are right!
