
Question Number 128439 by Study last updated on 07/Jan/21
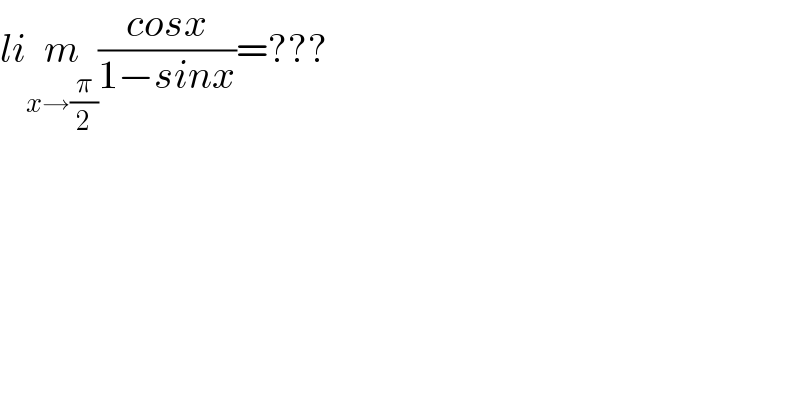
$${li}\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {{m}}\frac{{cosx}}{\mathrm{1}−{sinx}}=??? \\ $$
Answered by benjo_mathlover last updated on 07/Jan/21
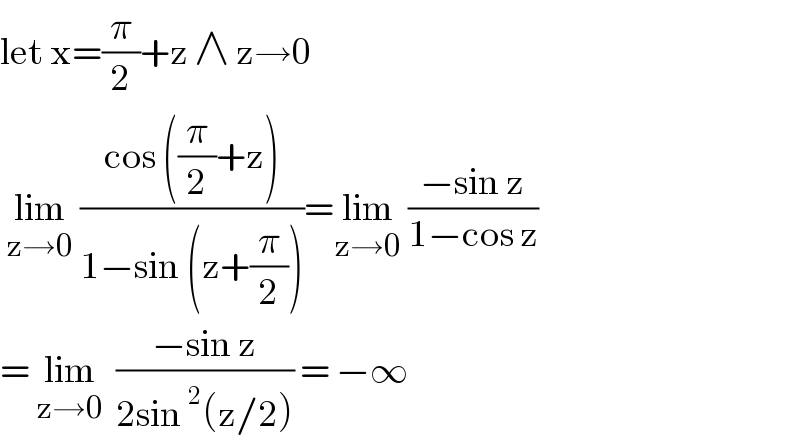
$$\mathrm{let}\:\mathrm{x}=\frac{\pi}{\mathrm{2}}+\mathrm{z}\:\wedge\:\mathrm{z}\rightarrow\mathrm{0} \\ $$$$\:\underset{\mathrm{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{cos}\:\left(\frac{\pi}{\mathrm{2}}+\mathrm{z}\right)}{\mathrm{1}−\mathrm{sin}\:\left(\mathrm{z}+\frac{\pi}{\mathrm{2}}\right)}=\underset{\mathrm{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{sin}\:\mathrm{z}}{\mathrm{1}−\mathrm{cos}\:\mathrm{z}} \\ $$$$=\:\underset{\mathrm{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{−\mathrm{sin}\:\mathrm{z}}{\mathrm{2sin}\:^{\mathrm{2}} \left(\mathrm{z}/\mathrm{2}\right)}\:=\:−\infty\: \\ $$
Answered by liberty last updated on 08/Jan/21

$$\:\underset{{x}\rightarrow\pi/\mathrm{2}} {\mathrm{lim}}\:\frac{\mathrm{cos}\:^{\mathrm{2}} \left(\mathrm{x}/\mathrm{2}\right)−\mathrm{sin}\:^{\mathrm{2}} \left(\mathrm{x}/\mathrm{2}\right)}{\mathrm{sin}\:^{\mathrm{2}} \left(\mathrm{x}/\mathrm{2}\right)−\mathrm{2sin}\:\left(\mathrm{x}/\mathrm{2}\right)\mathrm{cos}\:\left(\mathrm{x}/\mathrm{2}\right)+\mathrm{cos}\:^{\mathrm{2}} \left(\mathrm{x}/\mathrm{2}\right)} \\ $$$$=\:\underset{{x}\rightarrow\pi/\mathrm{2}} {\mathrm{lim}}\:\frac{\left(\mathrm{cos}\:\frac{\mathrm{x}}{\mathrm{2}}−\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{2}}\right)\left(\mathrm{cos}\:\frac{\mathrm{x}}{\mathrm{2}}+\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{2}}\right)}{\left(\mathrm{cos}\:\frac{\mathrm{x}}{\mathrm{2}}−\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$=\:\underset{{x}\rightarrow\pi/\mathrm{2}} {\mathrm{lim}}\:\frac{\mathrm{cos}\:\frac{\mathrm{x}}{\mathrm{2}}+\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{2}}}{\mid\mathrm{cos}\:\frac{\mathrm{x}}{\mathrm{2}}−\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{2}}\mid}\:=\:\frac{\sqrt{\mathrm{2}}}{\mathrm{0}}\:=\:\infty \\ $$$$\mathrm{or}\:\underset{{x}\rightarrow\pi/\mathrm{2}} {\mathrm{lim}}\frac{\mathrm{cos}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)+\mathrm{sin}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)}{\mid\mathrm{cos}\:\frac{\mathrm{x}}{\mathrm{2}}−\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{2}}\mid}=−\infty \\ $$
Answered by MJS_new last updated on 08/Jan/21
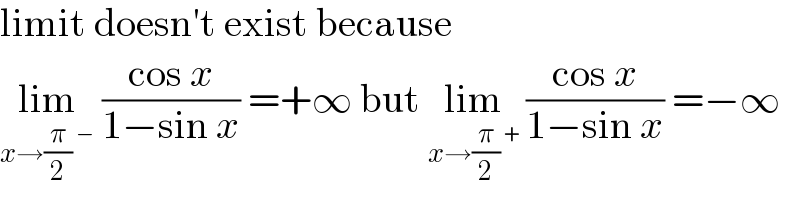
$$\mathrm{limit}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{exist}\:\mathrm{because} \\ $$$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}\:^{−} } {\mathrm{lim}}\:\frac{\mathrm{cos}\:{x}}{\mathrm{1}−\mathrm{sin}\:{x}}\:=+\infty\:\mathrm{but}\:\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}\:^{+} } {\mathrm{lim}}\:\frac{\mathrm{cos}\:{x}}{\mathrm{1}−\mathrm{sin}\:{x}}\:=−\infty \\ $$
Commented by liberty last updated on 08/Jan/21

$$\mathrm{yes}....\mathrm{agree} \\ $$
