Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 128290 by mr W last updated on 06/Jan/21

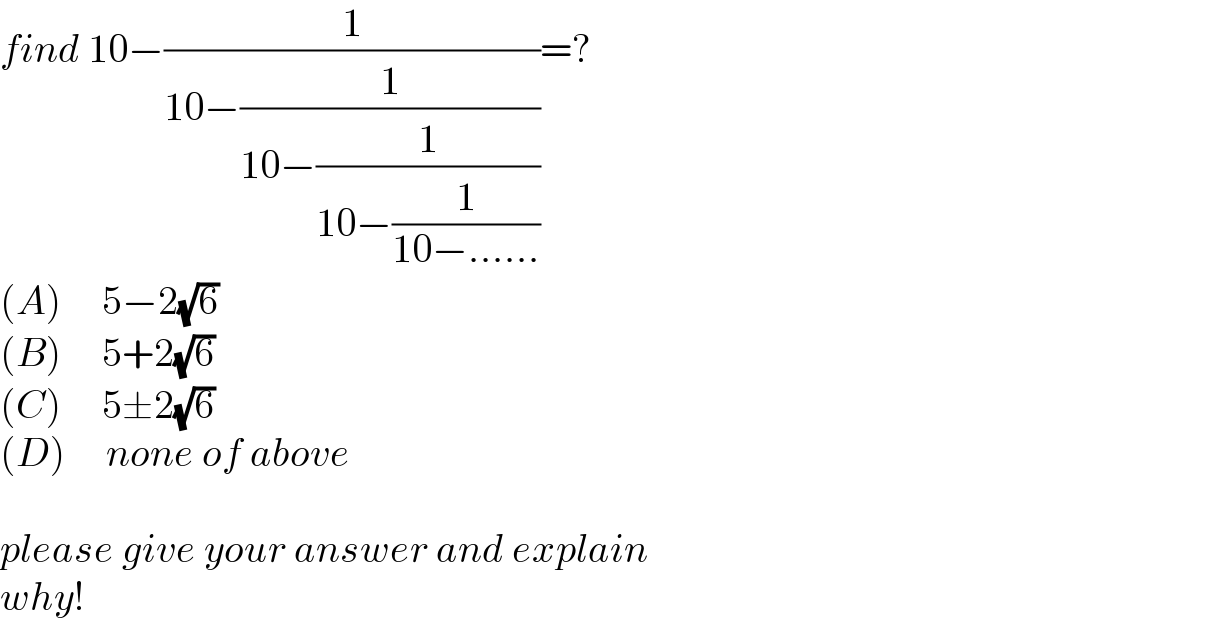
find 10−(1/(10−(1/(10−(1/(10−(1/(10−......))))))))=? (A) 5−2(√6) (B) 5+2(√6) (C) 5±2(√6) (D) none of above please give your answer and explain why!

$${find}\:\mathrm{10}−\frac{\mathrm{1}}{\mathrm{10}−\frac{\mathrm{1}}{\mathrm{10}−\frac{\mathrm{1}}{\mathrm{10}−\frac{\mathrm{1}}{\mathrm{10}−......}}}}=? \\ $$$$\left({A}\right)\:\:\:\:\:\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}} \\ $$$$\left({B}\right)\:\:\:\:\:\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}} \\ $$$$\left({C}\right)\:\:\:\:\:\mathrm{5}\pm\mathrm{2}\sqrt{\mathrm{6}} \\ $$$$\left({D}\right)\:\:\:\:\:{none}\:{of}\:{above} \\ $$$$ \\ $$$${please}\:{give}\:{your}\:{answer}\:{and}\:{explain} \\ $$$${why}! \\ $$

Commented by som(math1967) last updated on 06/Jan/21

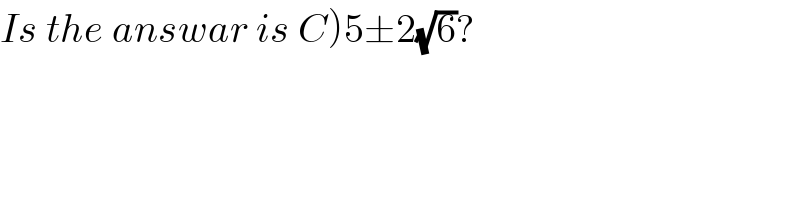
Is the answar is C)5±2(√6)?

$$\left.{Is}\:{the}\:{answar}\:{is}\:{C}\right)\mathrm{5}\pm\mathrm{2}\sqrt{\mathrm{6}}? \\ $$

Commented by som(math1967) last updated on 06/Jan/21

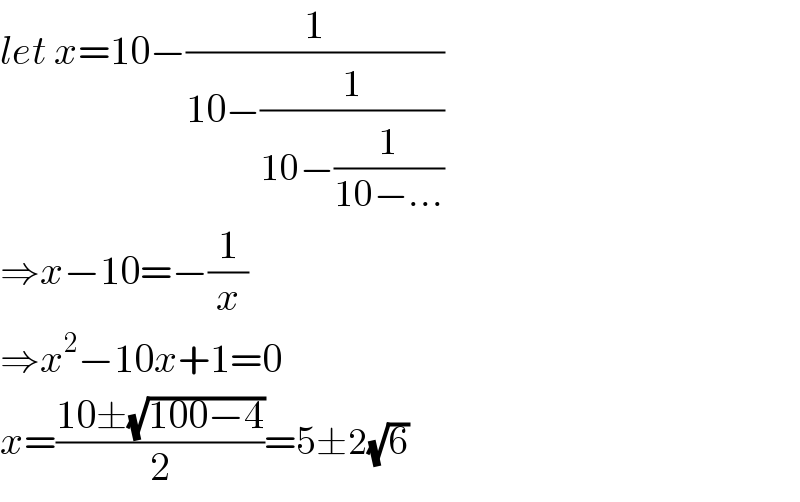
let x=10−(1/(10−(1/(10−(1/(10−...)))))) ⇒x−10=−(1/x) ⇒x^2 −10x+1=0 x=((10±(√(100−4)))/2)=5±2(√6)

$${let}\:{x}=\mathrm{10}−\frac{\mathrm{1}}{\mathrm{10}−\frac{\mathrm{1}}{\mathrm{10}−\frac{\mathrm{1}}{\mathrm{10}−...}}} \\ $$$$\Rightarrow{x}−\mathrm{10}=−\frac{\mathrm{1}}{{x}} \\ $$$$\Rightarrow{x}^{\mathrm{2}} −\mathrm{10}{x}+\mathrm{1}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{10}\pm\sqrt{\mathrm{100}−\mathrm{4}}}{\mathrm{2}}=\mathrm{5}\pm\mathrm{2}\sqrt{\mathrm{6}} \\ $$

Commented by Dwaipayan Shikari last updated on 06/Jan/21

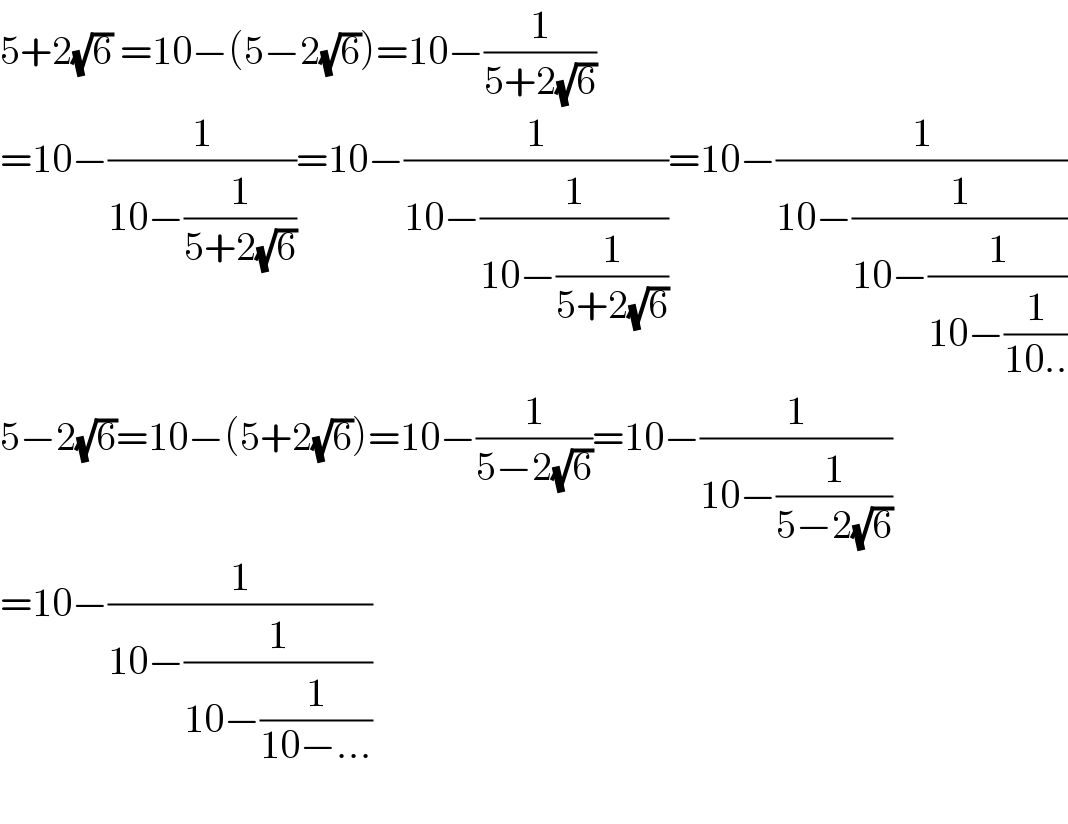
5+2(√6) =10−(5−2(√6))=10−(1/(5+2(√6))) =10−(1/(10−(1/(5+2(√6)))))=10−(1/(10−(1/(10−(1/(5+2(√6)))))))=10−(1/(10−(1/(10−(1/(10−(1/(10..)))))))) 5−2(√6)=10−(5+2(√6))=10−(1/(5−2(√6)))=10−(1/(10−(1/(5−2(√6))))) =10−(1/(10−(1/(10−(1/(10−...))))))

$$\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}\:=\mathrm{10}−\left(\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}}\right)=\mathrm{10}−\frac{\mathrm{1}}{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}} \\ $$$$=\mathrm{10}−\frac{\mathrm{1}}{\mathrm{10}−\frac{\mathrm{1}}{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}}}=\mathrm{10}−\frac{\mathrm{1}}{\mathrm{10}−\frac{\mathrm{1}}{\mathrm{10}−\frac{\mathrm{1}}{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}}}}=\mathrm{10}−\frac{\mathrm{1}}{\mathrm{10}−\frac{\mathrm{1}}{\mathrm{10}−\frac{\mathrm{1}}{\mathrm{10}−\frac{\mathrm{1}}{\mathrm{10}..}}}} \\ $$$$\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}}=\mathrm{10}−\left(\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}\right)=\mathrm{10}−\frac{\mathrm{1}}{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}}}=\mathrm{10}−\frac{\mathrm{1}}{\mathrm{10}−\frac{\mathrm{1}}{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}}}} \\ $$$$=\mathrm{10}−\frac{\mathrm{1}}{\mathrm{10}−\frac{\mathrm{1}}{\mathrm{10}−\frac{\mathrm{1}}{\mathrm{10}−...}}} \\ $$$$ \\ $$

Commented by mr W last updated on 06/Jan/21

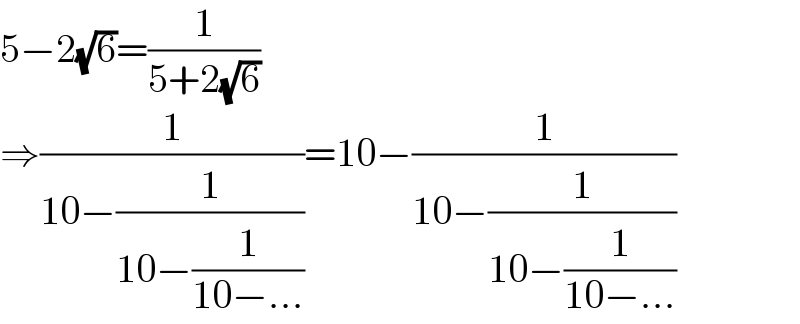
5−2(√6)=(1/(5+2(√6))) ⇒(1/(10−(1/(10−(1/(10−...))))))=10−(1/(10−(1/(10−(1/(10−...))))))

$$\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}}=\frac{\mathrm{1}}{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{10}−\frac{\mathrm{1}}{\mathrm{10}−\frac{\mathrm{1}}{\mathrm{10}−...}}}=\mathrm{10}−\frac{\mathrm{1}}{\mathrm{10}−\frac{\mathrm{1}}{\mathrm{10}−\frac{\mathrm{1}}{\mathrm{10}−...}}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com