
Previous in Differential Equation Next in Differential Equation
Question Number 128205 by john_santu last updated on 05/Jan/21
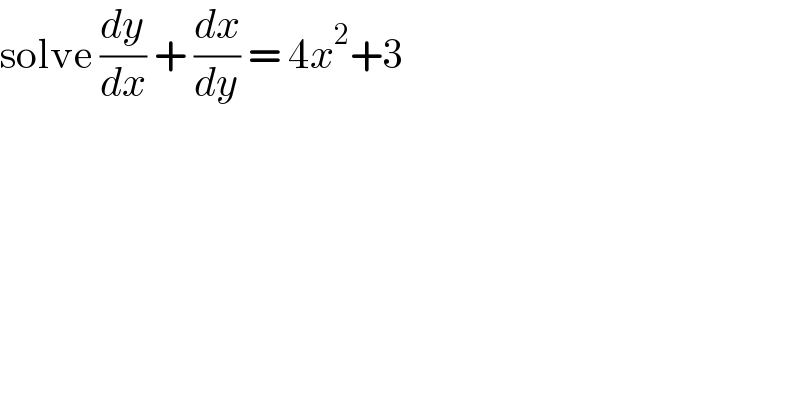
$$\mathrm{solve}\:\frac{{dy}}{{dx}}\:+\:\frac{{dx}}{{dy}}\:=\:\mathrm{4}{x}^{\mathrm{2}} +\mathrm{3} \\ $$
Answered by mr W last updated on 05/Jan/21
![(y′)^2 −(4x^2 +3)y′+1=0 y′=((4x^2 +3±(√((4x^2 +5)(4x^2 +1))))/2) y=(1/2)∫[4x^2 +3±(√((4x^2 +5)(4x^2 +1)))]dx y=(1/2)[((4x^3 )/3)+3x±(1/2)∫(√(((2x)^2 +5)((2x)^2 +1)))d(2x)] with u=2x y=((2x^3 )/3)+((3x)/2)±(1/4)∫(√((u^2 +5)(u^2 +1)))du ......](Q128206.png)
$$\left({y}'\right)^{\mathrm{2}} −\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{3}\right){y}'+\mathrm{1}=\mathrm{0} \\ $$$${y}'=\frac{\mathrm{4}{x}^{\mathrm{2}} +\mathrm{3}\pm\sqrt{\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{5}\right)\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{1}\right)}}{\mathrm{2}} \\ $$$${y}=\frac{\mathrm{1}}{\mathrm{2}}\int\left[\mathrm{4}{x}^{\mathrm{2}} +\mathrm{3}\pm\sqrt{\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{5}\right)\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{1}\right)}\right]{dx} \\ $$$${y}=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{4}{x}^{\mathrm{3}} }{\mathrm{3}}+\mathrm{3}{x}\pm\frac{\mathrm{1}}{\mathrm{2}}\int\sqrt{\left(\left(\mathrm{2}{x}\right)^{\mathrm{2}} +\mathrm{5}\right)\left(\left(\mathrm{2}{x}\right)^{\mathrm{2}} +\mathrm{1}\right)}{d}\left(\mathrm{2}{x}\right)\right] \\ $$$${with}\:{u}=\mathrm{2}{x} \\ $$$${y}=\frac{\mathrm{2}{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{3}{x}}{\mathrm{2}}\pm\frac{\mathrm{1}}{\mathrm{4}}\int\sqrt{\left({u}^{\mathrm{2}} +\mathrm{5}\right)\left({u}^{\mathrm{2}} +\mathrm{1}\right)}{du} \\ $$$$...... \\ $$
Commented by john_santu last updated on 05/Jan/21
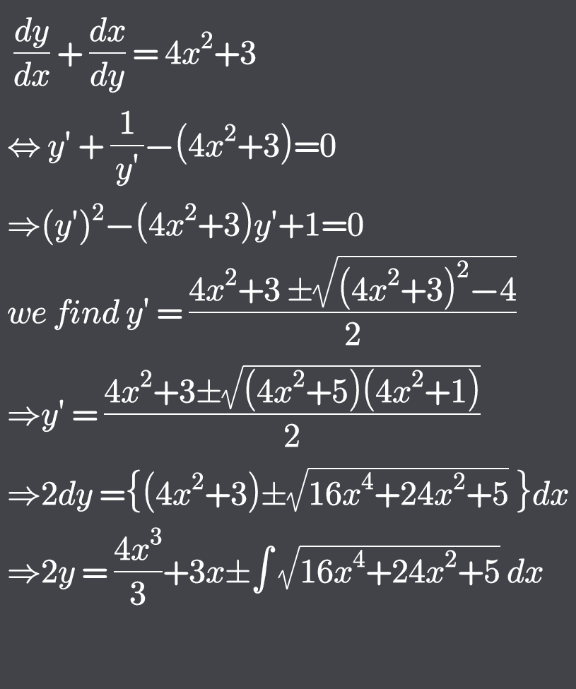
Commented by john_santu last updated on 05/Jan/21

$${i}\:{got}\:{the}\:{same}\:{result} \\ $$$${but}\:{stuck}\:{the}\:{second}\:{integral}\: \\ $$
Commented by mr W last updated on 05/Jan/21
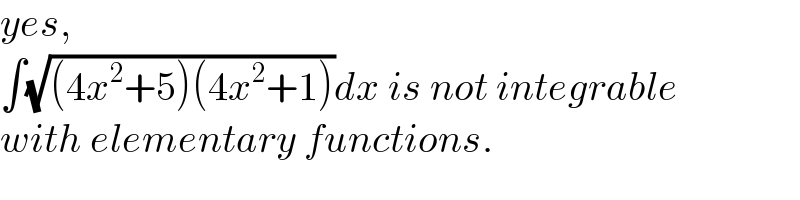
$${yes},\: \\ $$$$\int\sqrt{\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{5}\right)\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{1}\right)}{dx}\:{is}\:{not}\:{integrable} \\ $$$${with}\:{elementary}\:{functions}. \\ $$
Commented by mindispower last updated on 05/Jan/21

$${x}=\frac{\mathrm{1}}{\mathrm{2}}{sh}\left({t}\right) \\ $$$$\Rightarrow\int\sqrt{{sh}^{\mathrm{2}} \left({t}\right)+\mathrm{5}}.\frac{{ch}^{\mathrm{2}} \left({t}\right)}{\mathrm{2}}{dt} \\ $$$${ch}^{\mathrm{2}} \left({t}\right)=\frac{\mathrm{1}+{ch}\left(\mathrm{2}{t}\right)}{\mathrm{2}},\int{ch}^{\mathrm{2}} \left({t}\right)=\frac{{t}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}{sh}\left(\mathrm{2}{t}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{t}}{\mathrm{2}}+\frac{{sh}\left(\mathrm{2}{t}\right)}{\mathrm{4}}\right)\sqrt{{sh}^{\mathrm{2}} \left({t}\right)+\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{tsh}\left({t}\right){ch}\left({t}\right)}{\:\sqrt{{sh}^{\mathrm{2}} \left({t}\right)+\mathrm{5}}}{dt}−\frac{\mathrm{1}}{\mathrm{8}}\int\frac{{sh}^{\mathrm{2}} \left({t}\right)}{\:\sqrt{{sh}^{\mathrm{2}} \left({t}\right)+\mathrm{5}}}{dt} \\ $$$$\int\frac{{tsh}\left({t}\right){ch}\left({t}\right)}{\:\sqrt{{sh}^{\mathrm{2}} \left({t}\right)+\mathrm{5}}}{dt} \\ $$$$=\int\frac{{tsh}\left(\mathrm{2}{t}\right)}{\mathrm{2}.\sqrt{\mathrm{4}+{ch}^{\mathrm{2}} \left({t}\right)}}\:{by}\:{part}\:=\sqrt{\mathrm{4}+{ch}^{\mathrm{2}} \left({t}\right)}{t}−\int\sqrt{\mathrm{4}+{ch}^{\mathrm{2}} \left({t}\right)}{dt} \\ $$$$\int\sqrt{\mathrm{4}+{ch}^{\mathrm{2}} \left({t}\right)}{dt}=\int\sqrt{\mathrm{5}+{sh}^{\mathrm{2}} \left({t}\right)}{dt} \\ $$$${t}={iw} \\ $$$$\Rightarrow\int\sqrt{\mathrm{5}+\left({sh}\left({iw}\right)\right)^{\mathrm{2}} }.{idw} \\ $$$$={i}\int\sqrt{\mathrm{5}−{sin}^{\mathrm{2}} \left({w}\right)}{dw} \\ $$$$={i}\sqrt{\mathrm{5}}\int\sqrt{\mathrm{1}−\left(\frac{{sinw}}{\:\sqrt{\mathrm{5}}}\right)^{\mathrm{2}} }{dw}={i}\sqrt{\mathrm{5}}\left({E}\left({sin}\left({w},\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\right)\right)\right. \\ $$$${E}\left({sin}\left(\emptyset\right),{k}\right)=\int_{\mathrm{0}} ^{\varphi} \sqrt{\mathrm{1}−{k}^{\mathrm{2}} {sin}^{\mathrm{2}} \left({t}\right)}{dt}..\:\mathrm{2}\:{nd}\:{eleptic}\:{integrak} \\ $$$$\int\frac{{sh}^{\mathrm{2}} \left({t}\right)}{\:\sqrt{\mathrm{5}+{sh}^{\mathrm{2}} \left({t}\right)}},{dt}=\int\sqrt{{sh}^{\mathrm{2}} \left({t}\right)+\mathrm{5}}−\mathrm{5}\int\frac{{dt}}{\:\sqrt{\mathrm{5}+{sh}^{\mathrm{2}} \left({t}\right)}} \\ $$$${A}−\mathrm{5}{B},{A}\:{donne}\:{B},{t}\rightarrow{ix} \\ $$$${B}=\mathrm{5}{i}\int\frac{{dx}}{\:\sqrt{\mathrm{5}−{sin}^{\mathrm{2}} \left({x}\right)}}={i}\sqrt{\mathrm{5}}\int\frac{{dx}}{\:\sqrt{\mathrm{1}−\left(\frac{{sin}\left({x}\right)}{\:\sqrt{\mathrm{5}}}\right)^{\mathrm{2}} }} \\ $$$$={i}\sqrt{\mathrm{5}}{F}\left({sin}\left({x}\right),\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\right) \\ $$$${F}\left({sin}\left({t}\right),{k}\right)=\int\frac{{dt}}{\:\sqrt{\mathrm{1}−{k}^{\mathrm{2}} {sin}\left({x}\right)}},\:{first}\:{eleptic}\:{integral} \\ $$$$\Rightarrow\int\sqrt{\mathrm{5}+\mathrm{4}{x}^{\mathrm{2}} }.\sqrt{\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} }{dx}\:{has}\:{close}\:{hard}\:{to}\:{express} \\ $$$${withe}\:{x}\:{variable}\:{but}\:{possibl} \\ $$$$ \\ $$$$ \\ $$
Commented by john_santu last updated on 05/Jan/21

$${thank}\:{you} \\ $$
Commented by mindispower last updated on 06/Jan/21

$${withe}\:{pleasur} \\ $$
