
Question Number 128149 by MathSh last updated on 04/Jan/21
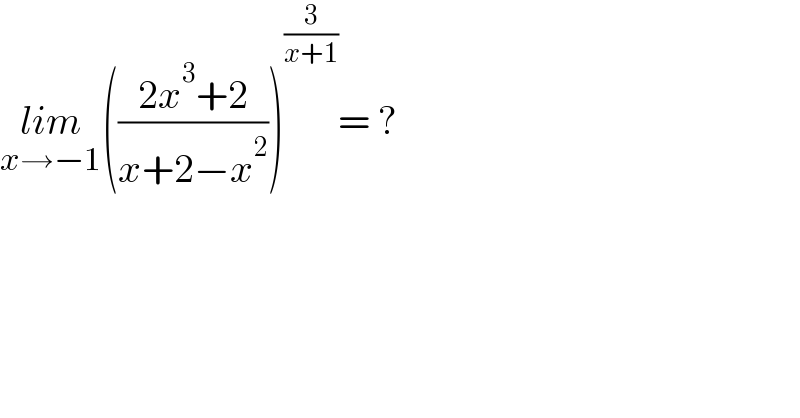
$$\underset{{x}\rightarrow−\mathrm{1}} {{lim}}\left(\frac{\mathrm{2}{x}^{\mathrm{3}} +\mathrm{2}}{{x}+\mathrm{2}−{x}^{\mathrm{2}} }\right)^{\frac{\mathrm{3}}{{x}+\mathrm{1}}} =\:? \\ $$
Answered by liberty last updated on 04/Jan/21
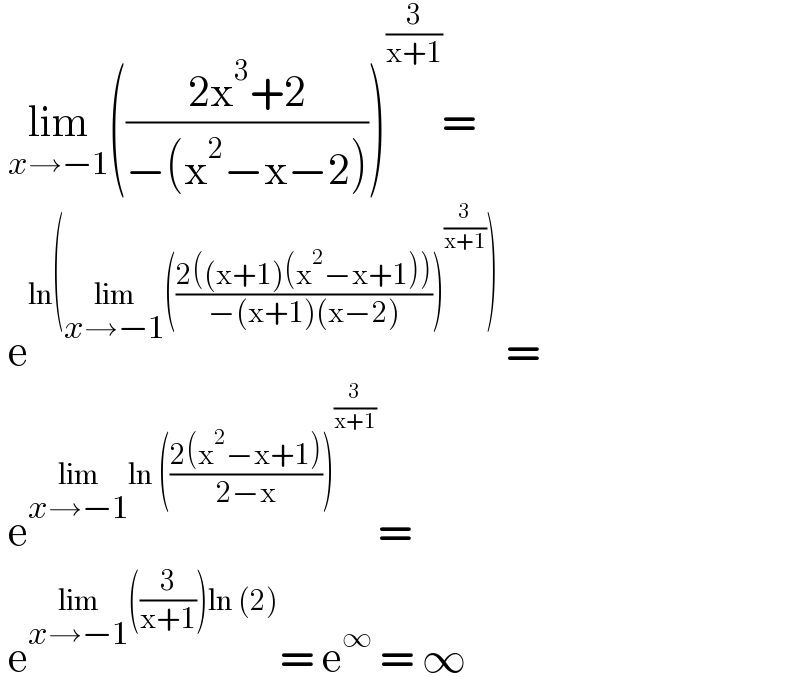
$$\:\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\left(\frac{\mathrm{2x}^{\mathrm{3}} +\mathrm{2}}{−\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{2}\right)}\right)^{\frac{\mathrm{3}}{\mathrm{x}+\mathrm{1}}} =\: \\ $$$$\:\mathrm{e}^{\mathrm{ln}\left(\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\left(\frac{\mathrm{2}\left(\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)\right)}{−\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}−\mathrm{2}\right)}\right)^{\frac{\mathrm{3}}{\mathrm{x}+\mathrm{1}}} \right)\:} = \\ $$$$\:\mathrm{e}^{\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}ln}\:\left(\frac{\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)}{\mathrm{2}−\mathrm{x}}\right)^{\frac{\mathrm{3}}{\mathrm{x}+\mathrm{1}}} } = \\ $$$$\:\mathrm{e}^{\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\left(\frac{\mathrm{3}}{\mathrm{x}+\mathrm{1}}\right)\mathrm{ln}\:\left(\mathrm{2}\right)} =\:\mathrm{e}^{\infty} \:=\:\infty \\ $$
