
Question Number 128094 by TITA last updated on 04/Jan/21
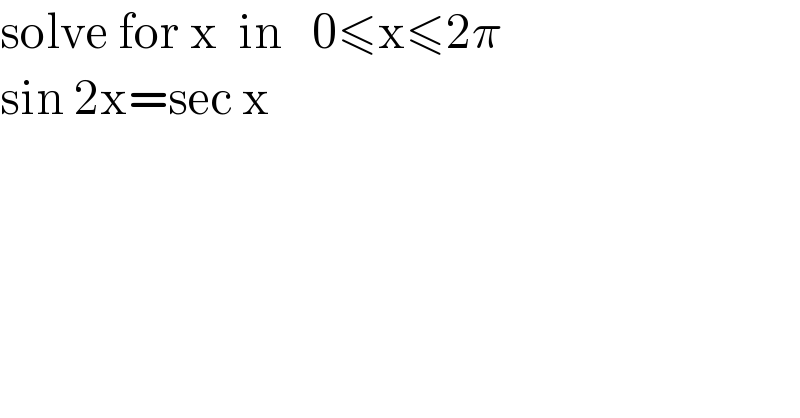
$$\mathrm{solve}\:\mathrm{for}\:\mathrm{x}\:\:\mathrm{in}\:\:\:\mathrm{0}\leqslant\mathrm{x}\leqslant\mathrm{2}\pi \\ $$$$\mathrm{sin}\:\mathrm{2x}=\mathrm{sec}\:\mathrm{x} \\ $$
Answered by MJS_new last updated on 04/Jan/21
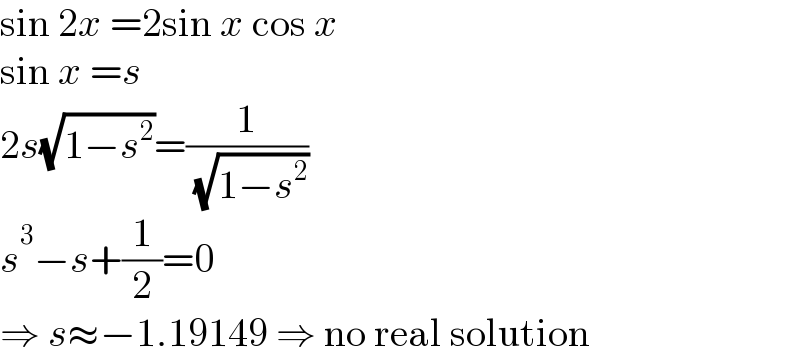
$$\mathrm{sin}\:\mathrm{2}{x}\:=\mathrm{2sin}\:{x}\:\mathrm{cos}\:{x} \\ $$$$\mathrm{sin}\:{x}\:={s} \\ $$$$\mathrm{2}{s}\sqrt{\mathrm{1}−{s}^{\mathrm{2}} }=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{s}^{\mathrm{2}} }} \\ $$$${s}^{\mathrm{3}} −{s}+\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{0} \\ $$$$\Rightarrow\:{s}\approx−\mathrm{1}.\mathrm{19149}\:\Rightarrow\:\mathrm{no}\:\mathrm{real}\:\mathrm{solution} \\ $$
