Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 127933 by AgnibhoMukhopadhyay last updated on 03/Jan/21

(1/((1/(x − 3)) + (1/(x + 4)))) If x > 0 and x ≠ 3, which of the following is equivalent to the expresion above? A. 2x + 1 B. x^2 + x − 12 C. ((x^2 + x − 12)/(2x + 1)) D. ((2x + 1)/(x^2 + x −12))

$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\frac{\mathrm{1}}{{x}\:−\:\mathrm{3}}\:+\:\frac{\mathrm{1}}{{x}\:+\:\mathrm{4}}} \\ $$ $$ \\ $$ $$\mathrm{If}\:{x}\:>\:\mathrm{0}\:\mathrm{and}\:{x}\:\neq\:\mathrm{3},\:\mathrm{which}\:\mathrm{of}\:\mathrm{the}\:\:\: \\ $$ $$\mathrm{following}\:\mathrm{is}\:\mathrm{equivalent}\:\mathrm{to}\:\mathrm{the}\: \\ $$ $$\mathrm{expresion}\:\mathrm{above}? \\ $$ $$\mathrm{A}.\:\:\mathrm{2}{x}\:+\:\mathrm{1} \\ $$ $$\mathrm{B}.\:\:{x}^{\mathrm{2}} \:+\:{x}\:−\:\mathrm{12}\: \\ $$ $$\mathrm{C}.\:\:\frac{{x}^{\mathrm{2}} \:+\:{x}\:−\:\mathrm{12}}{\mathrm{2}{x}\:+\:\mathrm{1}} \\ $$ $$\mathrm{D}.\:\:\frac{\mathrm{2}{x}\:+\:\mathrm{1}}{{x}^{\mathrm{2}} \:+\:{x}\:−\mathrm{12}} \\ $$

Answered by bramlexs22 last updated on 03/Jan/21

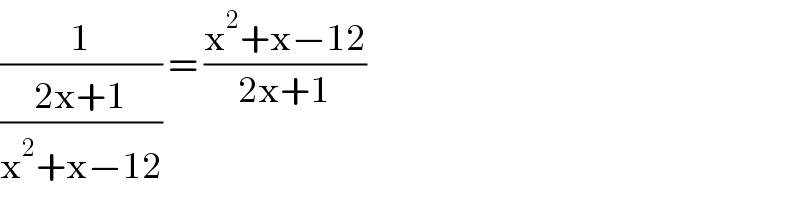
(1/((2x+1)/(x^2 +x−12))) = ((x^2 +x−12)/(2x+1))

$$\frac{\mathrm{1}}{\frac{\mathrm{2x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\mathrm{12}}}\:=\:\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\mathrm{12}}{\mathrm{2x}+\mathrm{1}}\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com