
Question Number 127912 by PRITHWISH SEN 2 last updated on 03/Jan/21

$$\mathrm{Dividing}\:\mathrm{by}\:\mathrm{the}\:\mathrm{factor}\:\mathrm{of}\:\mathrm{divisor}\:\mathrm{find}\:\mathrm{the}\: \\ $$$$\mathrm{quotient}\:\mathrm{and}\:\mathrm{remainder}\:\mathrm{of}\:\:\mathrm{715}\boldsymbol{\div}\mathrm{12} \\ $$
Answered by physicstutes last updated on 03/Jan/21

$$\:\mathrm{715}\:=\:\mathrm{12}\left(\mathrm{59}\right)\:+\:\mathrm{7} \\ $$$$\mathrm{remainder}\:=\:\mathrm{7} \\ $$
Commented by PRITHWISH SEN 2 last updated on 03/Jan/21

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{But}\:\mathrm{the}\:\mathrm{question}\:\mathrm{is}\:'\boldsymbol{\mathrm{division}}\:\boldsymbol{\mathrm{by}} \\ $$$$\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{factor}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{divisor}}'\:\mathrm{not}\:\mathrm{divide}\:\mathrm{by}\:\mathrm{the}\: \\ $$$$\mathrm{divisor}\:\mathrm{itself}. \\ $$
Commented by mr W last updated on 03/Jan/21
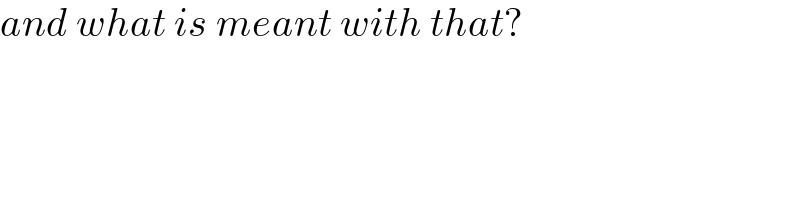
$${and}\:{what}\:{is}\:{meant}\:{with}\:{that}? \\ $$
Commented by PRITHWISH SEN 2 last updated on 03/Jan/21

$$\mathrm{actually}\:\mathrm{I}\:\mathrm{am}\:\mathrm{also}\:\mathrm{confused}.\:\mathrm{This}\:\mathrm{is}\:\mathrm{what}\:\mathrm{I}\:\mathrm{found} \\ $$$$\mathrm{on}\:\mathrm{a}\:\mathrm{5th}\:\mathrm{grade}\:\mathrm{maths}\:\mathrm{book}. \\ $$
Commented by mr W last updated on 03/Jan/21
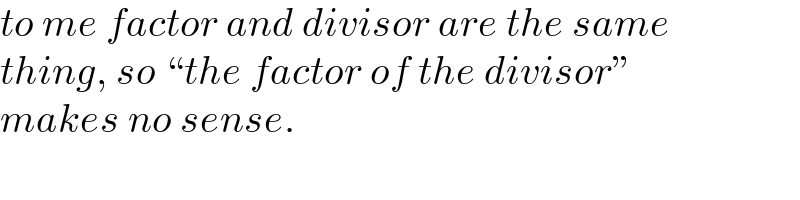
$${to}\:{me}\:{factor}\:{and}\:{divisor}\:{are}\:{the}\:{same} \\ $$$${thing},\:{so}\:``{the}\:{factor}\:{of}\:{the}\:{divisor}'' \\ $$$${makes}\:{no}\:{sense}. \\ $$
Commented by PRITHWISH SEN 2 last updated on 03/Jan/21

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by PRITHWISH SEN 2 last updated on 19/Jan/21
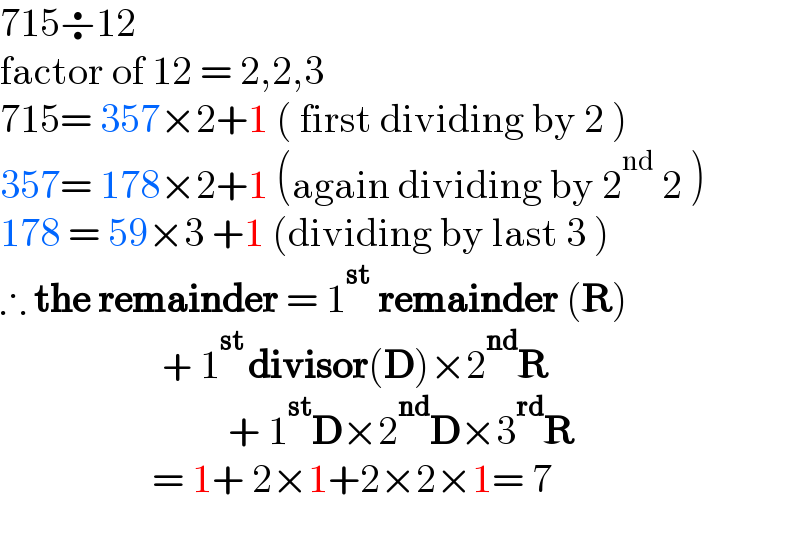
$$\mathrm{715}\boldsymbol{\div}\mathrm{12} \\ $$$$\mathrm{factor}\:\mathrm{of}\:\mathrm{12}\:=\:\mathrm{2},\mathrm{2},\mathrm{3} \\ $$$$\mathrm{715}=\:\mathrm{357}×\mathrm{2}+\mathrm{1}\:\left(\:\mathrm{first}\:\mathrm{dividing}\:\mathrm{by}\:\mathrm{2}\:\right) \\ $$$$\mathrm{357}=\:\mathrm{178}×\mathrm{2}+\mathrm{1}\:\left(\mathrm{again}\:\mathrm{dividing}\:\mathrm{by}\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{2}\:\right) \\ $$$$\mathrm{178}\:=\:\mathrm{59}×\mathrm{3}\:+\mathrm{1}\:\left(\mathrm{dividing}\:\mathrm{by}\:\mathrm{last}\:\mathrm{3}\:\right) \\ $$$$\therefore\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{remainder}}\:=\:\mathrm{1}^{\boldsymbol{\mathrm{st}}} \:\boldsymbol{\mathrm{remainder}}\:\left(\boldsymbol{\mathrm{R}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\:\mathrm{1}^{\boldsymbol{\mathrm{st}}\:} \boldsymbol{\mathrm{divisor}}\left(\boldsymbol{\mathrm{D}}\right)×\mathrm{2}^{\boldsymbol{\mathrm{nd}}} \boldsymbol{\mathrm{R}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\:\mathrm{1}^{\boldsymbol{\mathrm{st}}} \boldsymbol{\mathrm{D}}×\mathrm{2}^{\boldsymbol{\mathrm{nd}}} \boldsymbol{\mathrm{D}}×\mathrm{3}^{\boldsymbol{\mathrm{rd}}} \boldsymbol{\mathrm{R}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{1}+\:\mathrm{2}×\mathrm{1}+\mathrm{2}×\mathrm{2}×\mathrm{1}=\:\mathrm{7} \\ $$$$ \\ $$
