
Question Number 127652 by deleteduser12 last updated on 31/Dec/20

$${determine}\:{the}\:{coordinate}\:{of}\:{a}\:{point}\:{which}\:{is}\:{on}\:{the} \\ $$$$\mathrm{3}{x}−\mathrm{4}{y}+\mathrm{12}=\mathrm{0}\:{and}\:{the}\:{distance}\:{of}\:{the}\:{point}\:{from}\:\left(\mathrm{0},\mathrm{0}\right) \\ $$$${is}\:\mathrm{10}\:{unit} \\ $$
Answered by liberty last updated on 31/Dec/20
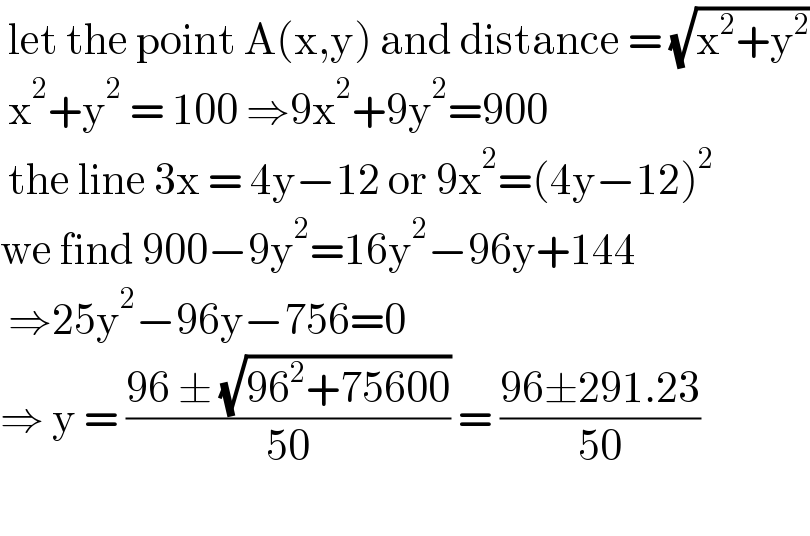
$$\:\mathrm{let}\:\mathrm{the}\:\mathrm{point}\:\mathrm{A}\left(\mathrm{x},\mathrm{y}\right)\:\mathrm{and}\:\mathrm{distance}\:=\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} } \\ $$$$\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \:=\:\mathrm{100}\:\Rightarrow\mathrm{9x}^{\mathrm{2}} +\mathrm{9y}^{\mathrm{2}} =\mathrm{900} \\ $$$$\:\mathrm{the}\:\mathrm{line}\:\mathrm{3x}\:=\:\mathrm{4y}−\mathrm{12}\:\mathrm{or}\:\mathrm{9x}^{\mathrm{2}} =\left(\mathrm{4y}−\mathrm{12}\right)^{\mathrm{2}} \\ $$$$\mathrm{we}\:\mathrm{find}\:\mathrm{900}−\mathrm{9y}^{\mathrm{2}} =\mathrm{16y}^{\mathrm{2}} −\mathrm{96y}+\mathrm{144} \\ $$$$\:\Rightarrow\mathrm{25y}^{\mathrm{2}} −\mathrm{96y}−\mathrm{756}=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{y}\:=\:\frac{\mathrm{96}\:\pm\:\sqrt{\mathrm{96}^{\mathrm{2}} +\mathrm{75600}}}{\mathrm{50}}\:=\:\frac{\mathrm{96}\pm\mathrm{291}.\mathrm{23}}{\mathrm{50}} \\ $$$$ \\ $$
