
Question Number 127644 by Dwaipayan Shikari last updated on 31/Dec/20
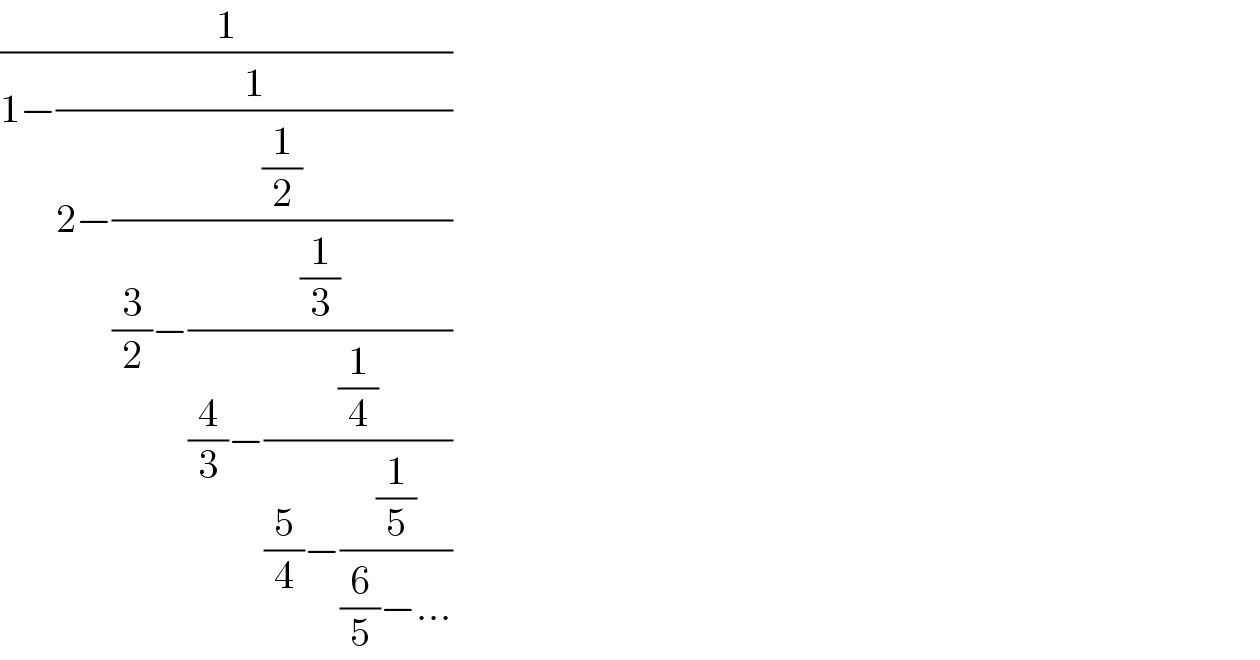
$$\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}−\frac{\frac{\mathrm{1}}{\mathrm{2}}}{\frac{\mathrm{3}}{\mathrm{2}}−\frac{\frac{\mathrm{1}}{\mathrm{3}}}{\frac{\mathrm{4}}{\mathrm{3}}−\frac{\frac{\mathrm{1}}{\mathrm{4}}}{\frac{\mathrm{5}}{\mathrm{4}}−\frac{\frac{\mathrm{1}}{\mathrm{5}}}{\frac{\mathrm{6}}{\mathrm{5}}−...}}}}}} \\ $$
Commented by Dwaipayan Shikari last updated on 31/Dec/20

$${a}_{\mathrm{0}} +{a}_{\mathrm{0}} {a}_{\mathrm{1}} +{a}_{\mathrm{0}} {a}_{\mathrm{2}} {a}_{\mathrm{1}} +{a}_{\mathrm{0}} {a}_{\mathrm{1}} {a}_{\mathrm{2}} {a}_{\mathrm{3}} +.....=\frac{{a}_{\mathrm{0}} }{\mathrm{1}−\frac{{a}_{\mathrm{1}} }{\mathrm{1}+{a}_{\mathrm{1}} −\frac{{a}_{\mathrm{2}} }{\mathrm{1}+{a}_{\mathrm{2}} −\frac{{a}_{\mathrm{3}} }{\mathrm{1}+{a}_{\mathrm{3}} −\frac{{a}_{\mathrm{4}} }{\mathrm{1}+{a}_{\mathrm{4}} ..}}}}} \\ $$$${e}^{{x}} =\mathrm{1}+{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{{x}^{\mathrm{3}} }{\mathrm{6}}+... \\ $$$$=\mathrm{1}+\mathrm{1}.{x}+{x}\left(\frac{{x}}{\mathrm{2}}\right)+{x}\left(\frac{{x}}{\mathrm{2}}\right)\left(\frac{{x}}{\mathrm{3}}\right)+{x}.\frac{{x}}{\mathrm{2}}.\frac{{x}}{\mathrm{3}}.\frac{{x}}{\mathrm{4}}+.. \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}−\frac{{x}}{\mathrm{1}+{x}−\frac{\frac{{x}}{\mathrm{2}}}{\mathrm{1}+\frac{{x}}{\mathrm{2}}−\frac{\frac{{x}}{\mathrm{3}}}{\mathrm{1}+\frac{{x}}{\mathrm{3}}−\frac{\frac{{x}}{\mathrm{4}}}{\mathrm{1}+\frac{{x}}{\mathrm{4}}−..}}}}} \\ $$$${e}=\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}−\frac{\frac{\mathrm{1}}{\mathrm{2}}}{\frac{\mathrm{3}}{\mathrm{2}}−\frac{\frac{\mathrm{1}}{\mathrm{3}}}{\frac{\mathrm{4}}{\mathrm{3}}−\frac{\frac{\mathrm{1}}{\mathrm{4}}}{\frac{\mathrm{5}}{\mathrm{4}}..}}}}} \\ $$
Commented by MathSh last updated on 31/Dec/20

$${e} \\ $$
