
Question Number 127604 by Algoritm last updated on 31/Dec/20

Answered by Lordose last updated on 31/Dec/20
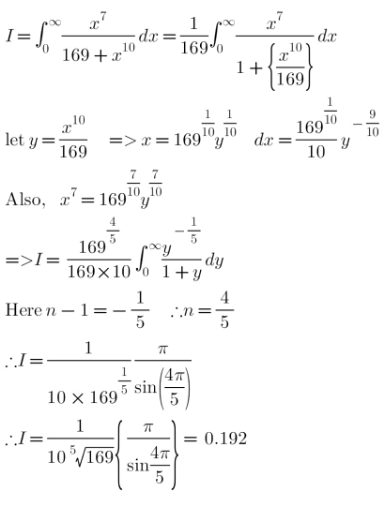
Commented by Algoritm last updated on 31/Dec/20

$$? \\ $$
Answered by MJS_new last updated on 31/Dec/20
![∫(x^7 /(x^(10) +a))dx= [t=x^2 → dx=(dt/(2x))] =(1/2)∫(t^3 /(t^5 +a))dt now you must decompose t^5 +a=(t+a^(1/5) )(t^2 −(((1−(√5))a^(1/5) )/2)t+a^(2/5) )(t^2 −(((1+(√5))a^(1/5) )/2)t+a^(2/5) )= [let α=a^(1/5) ∧β=((1−(√5))/2)∧γ=((1+(√5))/2)] =(t+α)(t^2 −αβt+α^2 )(t^2 −αγt+α^2 ) (1/2)∫(t^3 /((t+α)(t^2 −αβt+α^2 )(t^2 −αγt+α^2 )))dt= =I_1 +I_2 +I_3 +C I_1 =−(1/(2α(β+2)(γ+2)))∫(dt/(t+α)) I_2 =(1/(2α(β+2)(β−γ)))∫(((β+1)t−α)/(t^2 −αβt+α^2 ))dt I_3 =−(1/(2α(β−γ)(γ+2)))∫(((γ+1)t−α)/(t^2 −αγt+α^2 ))dt and these are easy to solve](Q127622.png)
$$\int\frac{{x}^{\mathrm{7}} }{{x}^{\mathrm{10}} +{a}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}={x}^{\mathrm{2}} \:\rightarrow\:{dx}=\frac{{dt}}{\mathrm{2}{x}}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{t}^{\mathrm{3}} }{{t}^{\mathrm{5}} +{a}}{dt} \\ $$$$\mathrm{now}\:\mathrm{you}\:\mathrm{must}\:\mathrm{decompose} \\ $$$${t}^{\mathrm{5}} +{a}=\left({t}+{a}^{\mathrm{1}/\mathrm{5}} \right)\left({t}^{\mathrm{2}} −\frac{\left(\mathrm{1}−\sqrt{\mathrm{5}}\right){a}^{\mathrm{1}/\mathrm{5}} }{\mathrm{2}}{t}+{a}^{\mathrm{2}/\mathrm{5}} \right)\left({t}^{\mathrm{2}} −\frac{\left(\mathrm{1}+\sqrt{\mathrm{5}}\right){a}^{\mathrm{1}/\mathrm{5}} }{\mathrm{2}}{t}+{a}^{\mathrm{2}/\mathrm{5}} \right)= \\ $$$$\:\:\:\:\:\left[\mathrm{let}\:\alpha={a}^{\mathrm{1}/\mathrm{5}} \wedge\beta=\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\wedge\gamma=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right] \\ $$$$=\left({t}+\alpha\right)\left({t}^{\mathrm{2}} −\alpha\beta{t}+\alpha^{\mathrm{2}} \right)\left({t}^{\mathrm{2}} −\alpha\gamma{t}+\alpha^{\mathrm{2}} \right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{t}^{\mathrm{3}} }{\left({t}+\alpha\right)\left({t}^{\mathrm{2}} −\alpha\beta{t}+\alpha^{\mathrm{2}} \right)\left({t}^{\mathrm{2}} −\alpha\gamma{t}+\alpha^{\mathrm{2}} \right)}{dt}= \\ $$$$={I}_{\mathrm{1}} +{I}_{\mathrm{2}} +{I}_{\mathrm{3}} +{C} \\ $$$${I}_{\mathrm{1}} =−\frac{\mathrm{1}}{\mathrm{2}\alpha\left(\beta+\mathrm{2}\right)\left(\gamma+\mathrm{2}\right)}\int\frac{{dt}}{{t}+\alpha} \\ $$$${I}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}\alpha\left(\beta+\mathrm{2}\right)\left(\beta−\gamma\right)}\int\frac{\left(\beta+\mathrm{1}\right){t}−\alpha}{{t}^{\mathrm{2}} −\alpha\beta{t}+\alpha^{\mathrm{2}} }{dt} \\ $$$${I}_{\mathrm{3}} =−\frac{\mathrm{1}}{\mathrm{2}\alpha\left(\beta−\gamma\right)\left(\gamma+\mathrm{2}\right)}\int\frac{\left(\gamma+\mathrm{1}\right){t}−\alpha}{{t}^{\mathrm{2}} −\alpha\gamma{t}+\alpha^{\mathrm{2}} }{dt} \\ $$$$\mathrm{and}\:\mathrm{these}\:\mathrm{are}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{solve} \\ $$
Commented by MJS_new last updated on 31/Dec/20

$$! \\ $$
