
Question Number 12760 by tawa last updated on 30/Apr/17

Answered by mrW1 last updated on 01/May/17
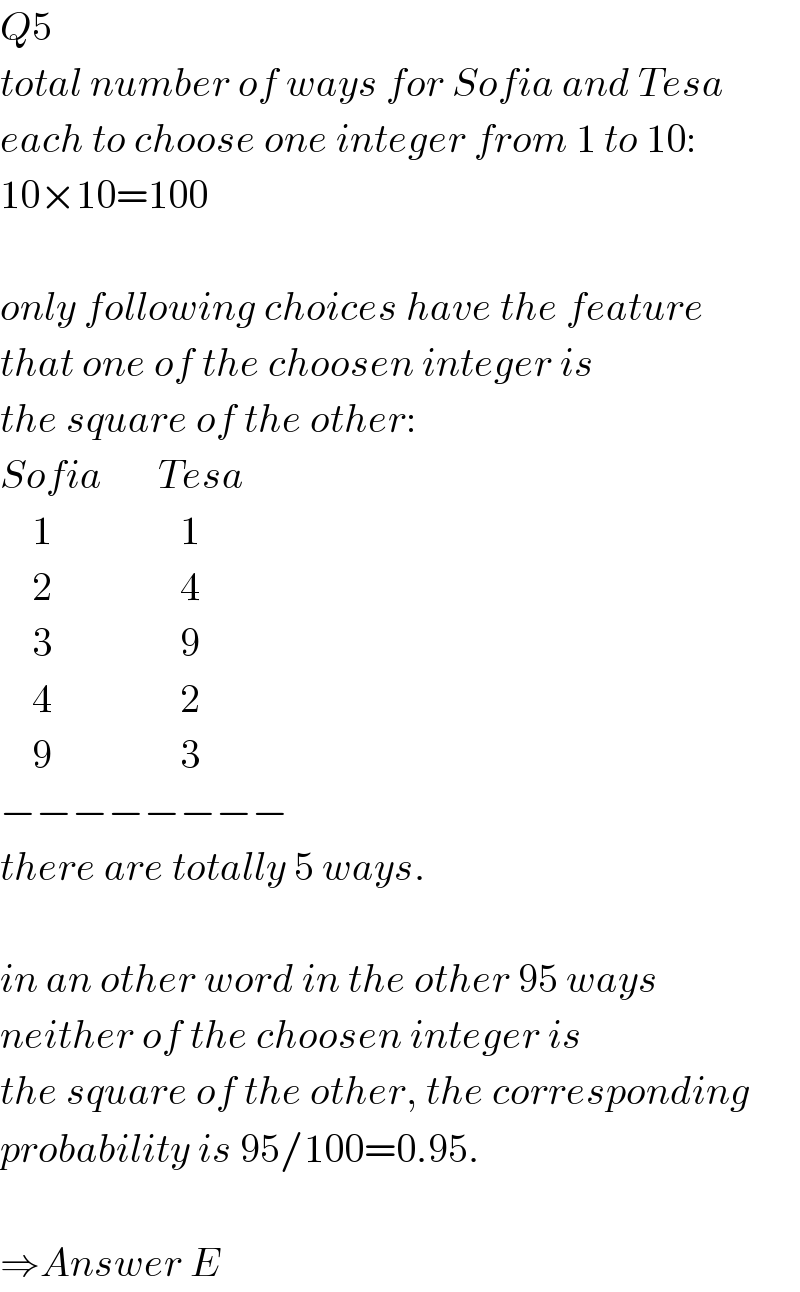
$${Q}\mathrm{5} \\ $$$${total}\:{number}\:{of}\:{ways}\:{for}\:{Sofia}\:{and}\:{Tesa}\: \\ $$$${each}\:{to}\:{choose}\:{one}\:{integer}\:{from}\:\mathrm{1}\:{to}\:\mathrm{10}: \\ $$$$\mathrm{10}×\mathrm{10}=\mathrm{100} \\ $$$$ \\ $$$${only}\:{following}\:{choices}\:{have}\:{the}\:{feature} \\ $$$${that}\:{one}\:{of}\:{the}\:{choosen}\:{integer}\:{is} \\ $$$${the}\:{square}\:{of}\:{the}\:{other}: \\ $$$${Sofia}\:\:\:\:\:\:\:{Tesa} \\ $$$$\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1} \\ $$$$\:\:\:\:\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{4} \\ $$$$\:\:\:\:\mathrm{3}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{9} \\ $$$$\:\:\:\:\mathrm{4}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2} \\ $$$$\:\:\:\:\mathrm{9}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3} \\ $$$$−−−−−−−− \\ $$$${there}\:{are}\:{totally}\:\mathrm{5}\:{ways}. \\ $$$$ \\ $$$${in}\:{an}\:{other}\:{word}\:{in}\:{the}\:{other}\:\mathrm{95}\:{ways} \\ $$$${neither}\:{of}\:{the}\:{choosen}\:{integer}\:{is} \\ $$$${the}\:{square}\:{of}\:{the}\:{other},\:{the}\:{corresponding} \\ $$$${probability}\:{is}\:\mathrm{95}/\mathrm{100}=\mathrm{0}.\mathrm{95}. \\ $$$$ \\ $$$$\Rightarrow{Answer}\:{E} \\ $$
Commented by tawa last updated on 01/May/17
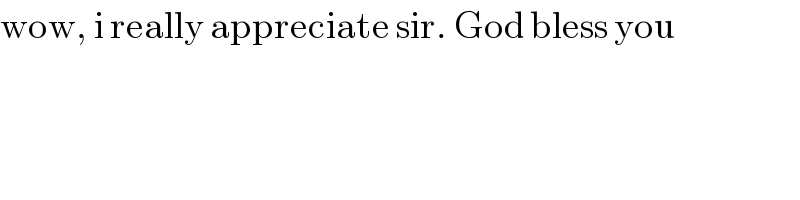
$$\mathrm{wow},\:\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you} \\ $$
Answered by mrW1 last updated on 01/May/17
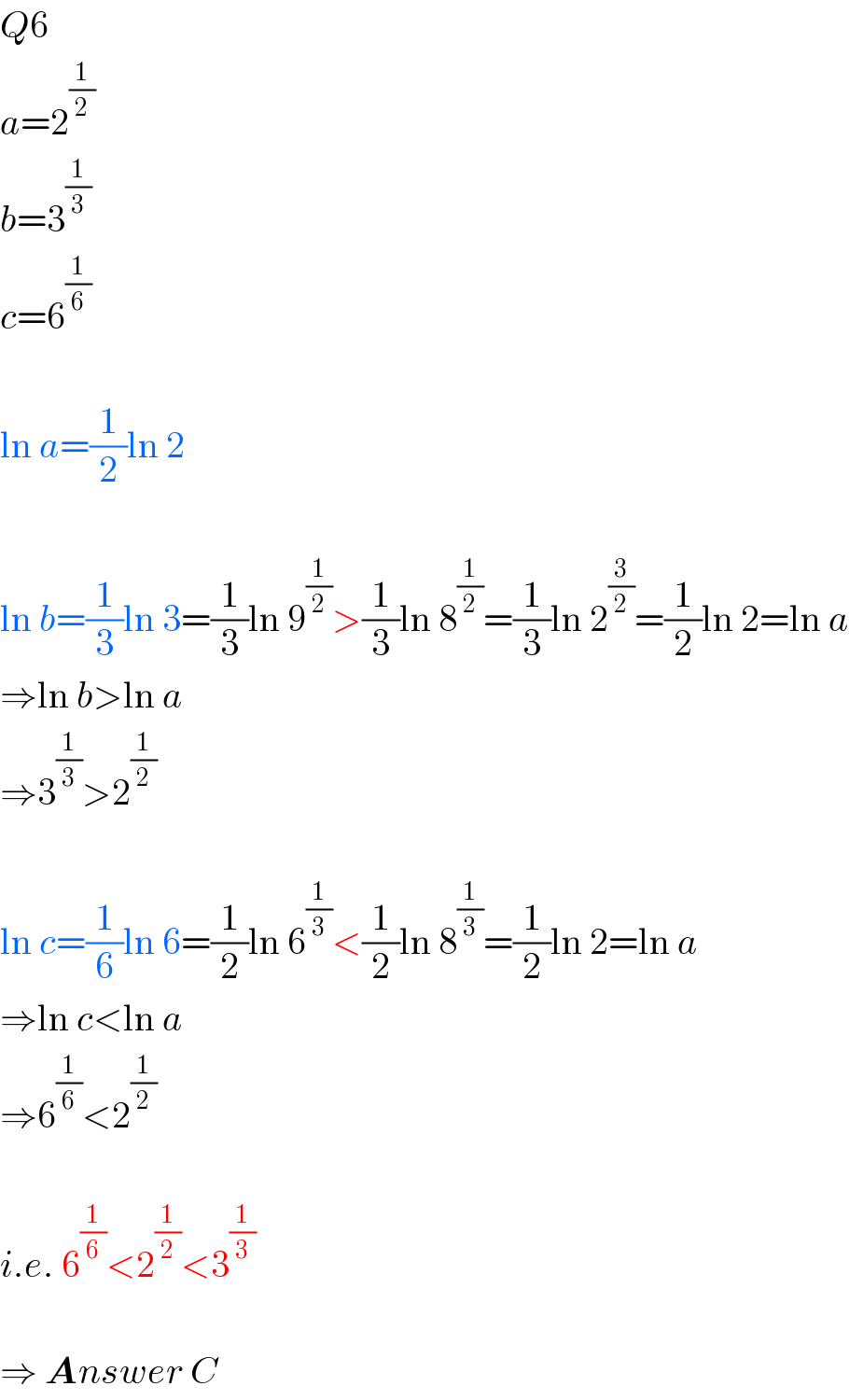
$${Q}\mathrm{6} \\ $$$${a}=\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$${b}=\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$${c}=\mathrm{6}^{\frac{\mathrm{1}}{\mathrm{6}}} \\ $$$$ \\ $$$$\mathrm{ln}\:{a}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mathrm{2} \\ $$$$ \\ $$$$\mathrm{ln}\:{b}=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\:\mathrm{3}=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\:\mathrm{9}^{\frac{\mathrm{1}}{\mathrm{2}}} >\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\:\mathrm{8}^{\frac{\mathrm{1}}{\mathrm{2}}} =\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\:\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{2}}} =\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mathrm{2}=\mathrm{ln}\:{a} \\ $$$$\Rightarrow\mathrm{ln}\:{b}>\mathrm{ln}\:{a} \\ $$$$\Rightarrow\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{3}}} >\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$ \\ $$$$\mathrm{ln}\:{c}=\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\:\mathrm{6}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mathrm{6}^{\frac{\mathrm{1}}{\mathrm{3}}} <\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mathrm{8}^{\frac{\mathrm{1}}{\mathrm{3}}} =\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mathrm{2}=\mathrm{ln}\:{a} \\ $$$$\Rightarrow\mathrm{ln}\:{c}<\mathrm{ln}\:{a} \\ $$$$\Rightarrow\mathrm{6}^{\frac{\mathrm{1}}{\mathrm{6}}} <\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$ \\ $$$${i}.{e}.\:\mathrm{6}^{\frac{\mathrm{1}}{\mathrm{6}}} <\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{2}}} <\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$ \\ $$$$\Rightarrow\:\boldsymbol{{A}}{nswer}\:{C} \\ $$
Commented by tawa last updated on 01/May/17
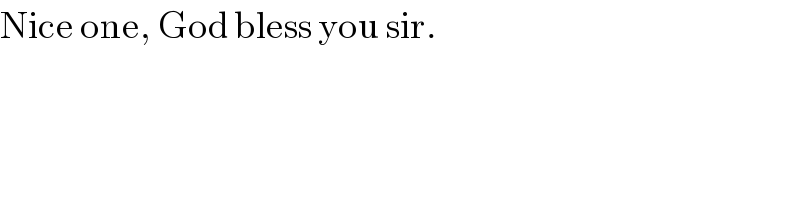
$$\mathrm{Nice}\:\mathrm{one},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
