
Previous in Differential Equation Next in Differential Equation
Question Number 127589 by bramlexs22 last updated on 31/Dec/20
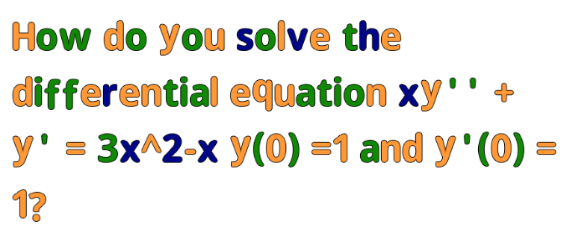
Answered by liberty last updated on 31/Dec/20

$$\left(\bullet\right)\:\mathrm{let}\:\mathrm{y}'=\mathrm{z}\:\Rightarrow\:\mathrm{xz}'\:+\:\mathrm{z}\:=\:\mathrm{3x}^{\mathrm{2}} −\mathrm{x}\: \\ $$$$\:\:\:\:\frac{\mathrm{d}}{\mathrm{dx}}\:\left(\mathrm{xz}\right)\:=\:\mathrm{3x}^{\mathrm{2}} −\mathrm{x}\: \\ $$$$\:\:\:\mathrm{xz}\:=\:\mathrm{x}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} \:+\mathrm{C}_{\mathrm{1}} \\ $$$$\:\:\:\:\mathrm{z}\:=\:\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\:+\:\frac{\mathrm{C}_{\mathrm{1}} }{\mathrm{x}} \\ $$$$\:\:\:\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}+\:\frac{\mathrm{C}_{\mathrm{1}} }{\mathrm{x}} \\ $$$$\:\:\:\:\mathrm{y}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{4}}\mathrm{x}^{\mathrm{2}} +\:\mathrm{C}_{\mathrm{1}} \mathrm{ln}\:\mid\mathrm{x}\mid\:+\:\mathrm{C}_{\mathrm{2}} \\ $$$$\mathrm{apply}\:\mathrm{the}\:\mathrm{initial}\:\mathrm{condition}\:\mathrm{y}\left(\mathrm{0}\right)=\mathrm{1}\:\mathrm{and}\:\mathrm{y}'\left(\mathrm{0}\right)=\mathrm{1} \\ $$$$\:\:\mathrm{start}\:\mathrm{with}\:\mathrm{the}\:\mathrm{first}\:\mathrm{derivative}\: \\ $$$$\:\mathrm{0}.\mathrm{1}\:=\:\mathrm{0}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{2}}.\mathrm{0}^{\mathrm{2}} \:+\:\mathrm{C}_{\mathrm{1}} \:\Rightarrow\mathrm{C}_{\mathrm{1}} =\mathrm{0}\: \\ $$$$\mathrm{and}\:\mathrm{1}\:=\:\frac{\mathrm{0}^{\mathrm{3}} }{\mathrm{3}}−\frac{\mathrm{0}^{\mathrm{4}} }{\mathrm{4}}+\mathrm{C}_{\mathrm{2}} \:\Rightarrow\mathrm{C}_{\mathrm{2}} =\mathrm{1} \\ $$$$\therefore\:\mathrm{y}\:=\:\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{4}}+\mathrm{1}\: \\ $$
