
Question Number 127575 by Ar Brandon last updated on 30/Dec/20
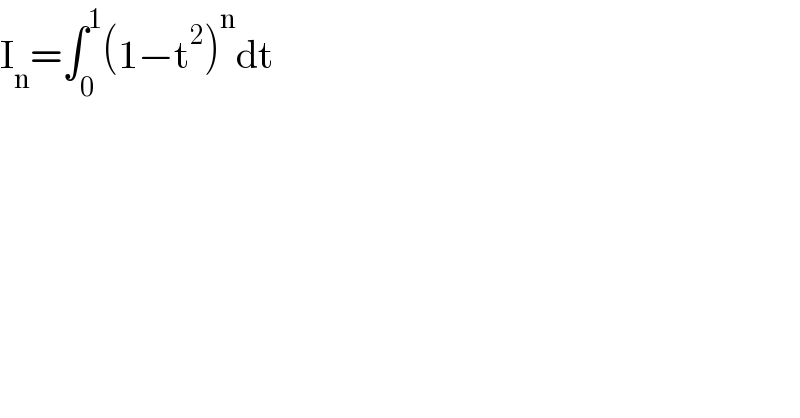
$$\mathrm{I}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{n}} \mathrm{dt} \\ $$
Answered by Ar Brandon last updated on 30/Dec/20
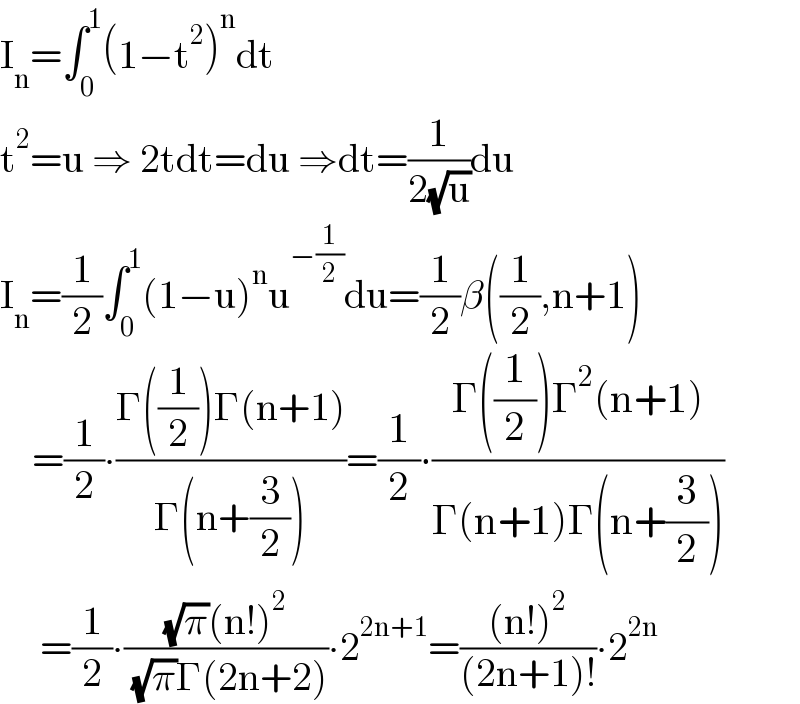
$$\mathrm{I}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{n}} \mathrm{dt} \\ $$$$\mathrm{t}^{\mathrm{2}} =\mathrm{u}\:\Rightarrow\:\mathrm{2tdt}=\mathrm{du}\:\Rightarrow\mathrm{dt}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{u}}}\mathrm{du} \\ $$$$\mathrm{I}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−\mathrm{u}\right)^{\mathrm{n}} \mathrm{u}^{−\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{du}=\frac{\mathrm{1}}{\mathrm{2}}\beta\left(\frac{\mathrm{1}}{\mathrm{2}},\mathrm{n}+\mathrm{1}\right) \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\centerdot\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\mathrm{n}+\mathrm{1}\right)}{\Gamma\left(\mathrm{n}+\frac{\mathrm{3}}{\mathrm{2}}\right)}=\frac{\mathrm{1}}{\mathrm{2}}\centerdot\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma^{\mathrm{2}} \left(\mathrm{n}+\mathrm{1}\right)}{\Gamma\left(\mathrm{n}+\mathrm{1}\right)\Gamma\left(\mathrm{n}+\frac{\mathrm{3}}{\mathrm{2}}\right)} \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\centerdot\frac{\sqrt{\pi}\left(\mathrm{n}!\right)^{\mathrm{2}} }{\:\sqrt{\pi}\Gamma\left(\mathrm{2n}+\mathrm{2}\right)}\centerdot\mathrm{2}^{\mathrm{2n}+\mathrm{1}} =\frac{\left(\mathrm{n}!\right)^{\mathrm{2}} }{\left(\mathrm{2n}+\mathrm{1}\right)!}\centerdot\mathrm{2}^{\mathrm{2n}} \\ $$
