
Question Number 127540 by mathocean1 last updated on 30/Dec/20
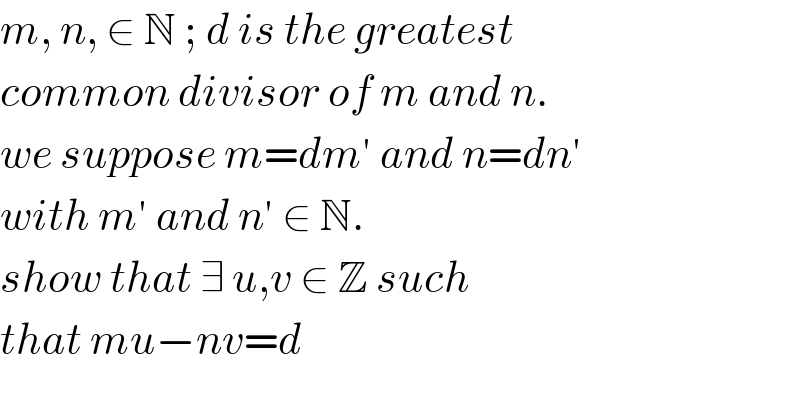
$${m},\:{n},\:\in\:\mathbb{N}\:;\:{d}\:{is}\:{the}\:{greatest} \\ $$$${common}\:{divisor}\:{of}\:{m}\:{and}\:{n}.\: \\ $$$${we}\:{suppose}\:{m}={dm}'\:{and}\:{n}={dn}'\: \\ $$$${with}\:{m}'\:{and}\:{n}'\:\in\:\mathbb{N}. \\ $$$${show}\:{that}\:\exists\:{u},{v}\:\in\:\mathbb{Z}\:{such}\: \\ $$$${that}\:{mu}−{nv}={d} \\ $$
