
Question Number 12724 by b.e.h.i.8.3.4.1.7@gmail.com last updated on 29/Apr/17
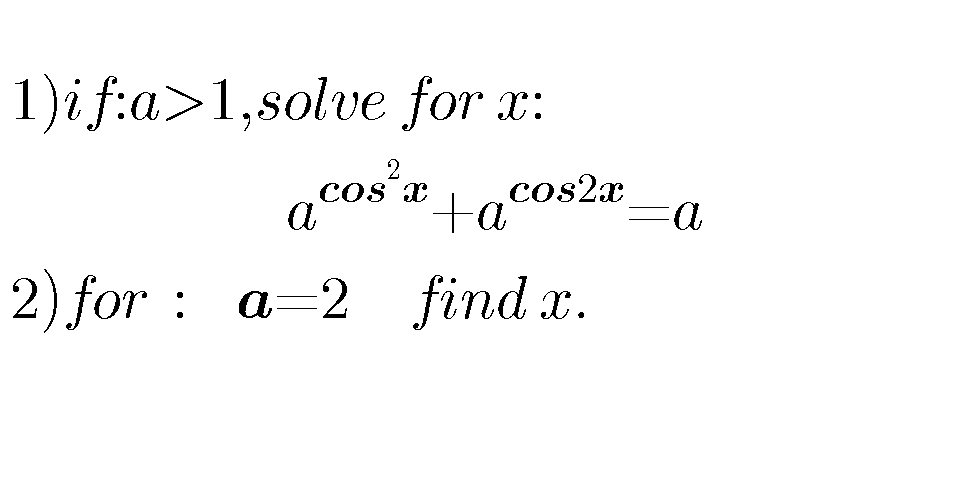
Answered by sma3l2996 last updated on 30/Apr/17

$${a}^{{cos}^{\mathrm{2}} {x}} +{a}^{\mathrm{2}{cos}^{\mathrm{2}} {x}−\mathrm{1}} ={a} \\ $$$${a}^{{cos}^{\mathrm{2}} {x}} +\left({a}^{{cos}^{\mathrm{2}} {x}} \right)^{\mathrm{2}} ×{a}^{−\mathrm{1}} ={a} \\ $$$$\left({a}^{{cos}^{\mathrm{2}} {x}} \right)^{\mathrm{2}} +{a}×{a}^{{cos}^{\mathrm{2}} {x}} ={a}^{\mathrm{2}} \\ $$$$\left({a}^{{cos}^{\mathrm{2}} {x}} \right)^{\mathrm{2}} +\mathrm{2}×\frac{{a}}{\mathrm{2}}×{a}^{{cos}^{\mathrm{2}} {x}} +\left(\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} =\left(\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} +{a}^{\mathrm{2}} \\ $$$$\left({a}^{{cos}^{\mathrm{2}} {x}} +\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{\mathrm{5}}{\mathrm{4}}{a}^{\mathrm{2}} \\ $$$${a}^{{cos}^{\mathrm{2}} {x}} +\frac{{a}}{\mathrm{2}}=\underset{−} {+}\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}{a} \\ $$$${a}^{{cos}^{\mathrm{2}} {x}} =−\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}{a}\:\:\:{or}\:\:{a}^{{cos}^{\mathrm{2}} {x}} =\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}{a} \\ $$$${cos}^{\mathrm{2}} {x}={log}_{{a}} \left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}{a}\right) \\ $$$${x}={acos}\left(\sqrt{{log}_{{a}} \left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}{a}\right)}\right)+\mathrm{2}{k}\pi\:\:\:\backslash{k}=\left(\mathrm{0},\mathrm{1},\mathrm{2},...\right) \\ $$$${for}\:{a}=\mathrm{2} \\ $$$${x}={acos}\left(\sqrt{{log}_{\mathrm{2}} \left(\sqrt{\mathrm{5}}−\mathrm{1}\right)}\right)+\mathrm{2}{k}\pi\:\:\backslash{k}=\left(\mathrm{0},\mathrm{1},\mathrm{2},...\right) \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 30/Apr/17
$${thank}\:{you}\:{so}\:{much}. \\ $$
