
Question Number 127139 by MathSh last updated on 27/Dec/20
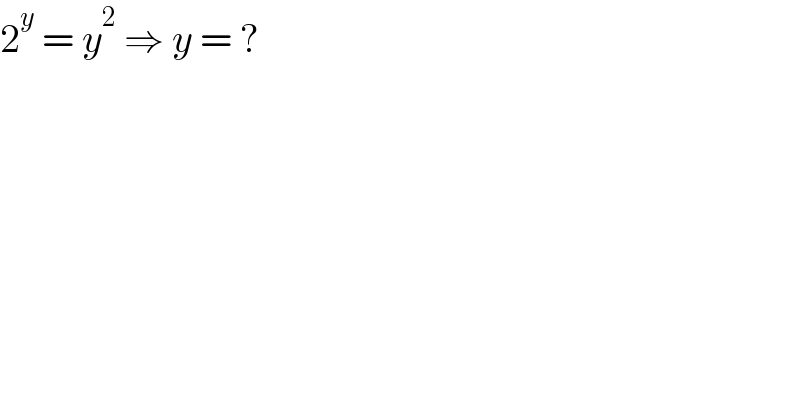
$$\mathrm{2}^{{y}} \:=\:{y}^{\mathrm{2}} \:\Rightarrow\:{y}\:=\:? \\ $$
Answered by Ar Brandon last updated on 27/Dec/20

$$\mathrm{2} \\ $$
Commented by MathSh last updated on 27/Dec/20
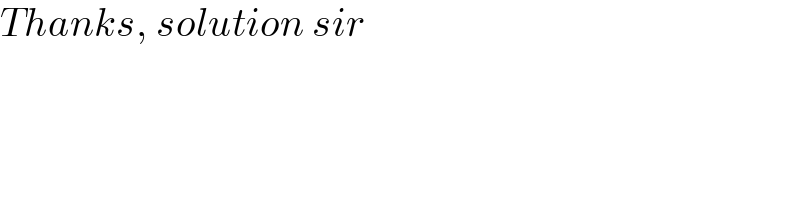
$${Thanks},\:{solution}\:{sir} \\ $$
Answered by Dwaipayan Shikari last updated on 27/Dec/20
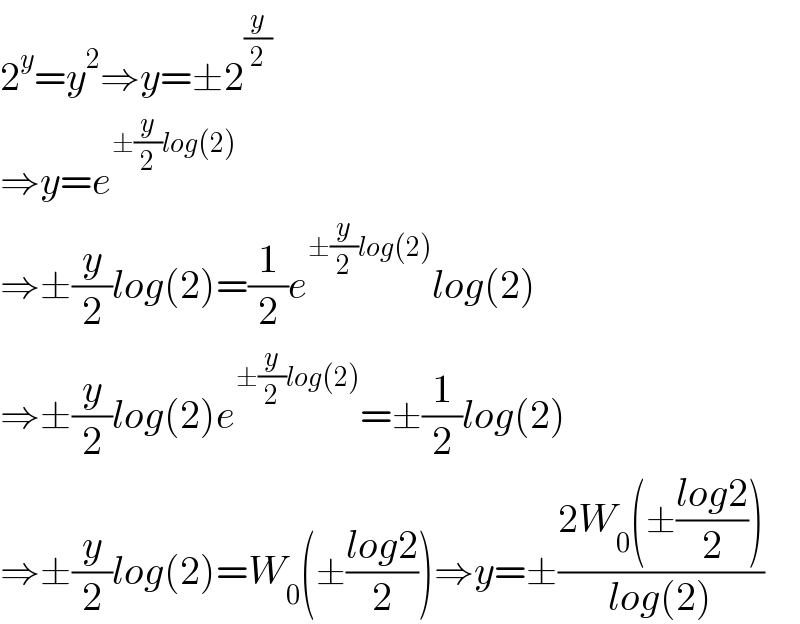
$$\mathrm{2}^{{y}} ={y}^{\mathrm{2}} \Rightarrow{y}=\pm\mathrm{2}^{\frac{{y}}{\mathrm{2}}} \\ $$$$\Rightarrow{y}={e}^{\pm\frac{{y}}{\mathrm{2}}{log}\left(\mathrm{2}\right)} \\ $$$$\Rightarrow\pm\frac{{y}}{\mathrm{2}}{log}\left(\mathrm{2}\right)=\frac{\mathrm{1}}{\mathrm{2}}{e}^{\pm\frac{{y}}{\mathrm{2}}{log}\left(\mathrm{2}\right)} {log}\left(\mathrm{2}\right) \\ $$$$\Rightarrow\pm\frac{{y}}{\mathrm{2}}{log}\left(\mathrm{2}\right){e}^{\pm\frac{{y}}{\mathrm{2}}{log}\left(\mathrm{2}\right)} =\pm\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\mathrm{2}\right) \\ $$$$\Rightarrow\pm\frac{{y}}{\mathrm{2}}{log}\left(\mathrm{2}\right)={W}_{\mathrm{0}} \left(\pm\frac{{log}\mathrm{2}}{\mathrm{2}}\right)\Rightarrow{y}=\pm\frac{\mathrm{2}{W}_{\mathrm{0}} \left(\pm\frac{{log}\mathrm{2}}{\mathrm{2}}\right)}{{log}\left(\mathrm{2}\right)} \\ $$
Commented by MathSh last updated on 27/Dec/20
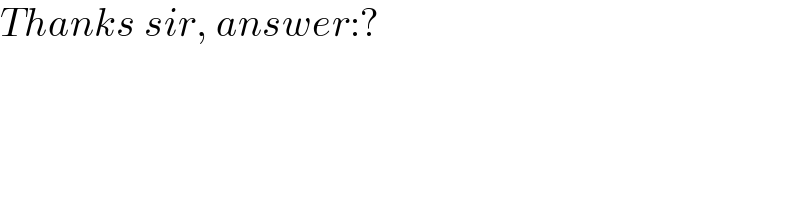
$${Thanks}\:{sir},\:{answer}:? \\ $$
