
Question Number 127109 by mohammad17 last updated on 26/Dec/20
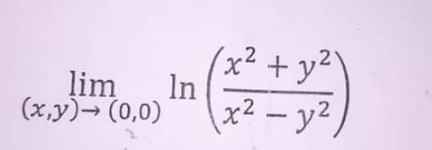
Answered by Ar Brandon last updated on 27/Dec/20
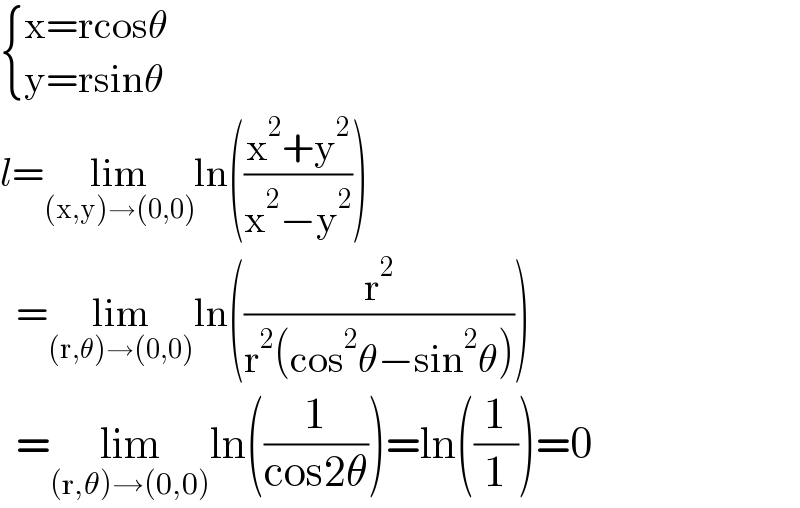
$$\begin{cases}{\mathrm{x}=\mathrm{rcos}\theta}\\{\mathrm{y}=\mathrm{rsin}\theta}\end{cases} \\ $$$${l}=\underset{\left(\mathrm{x},\mathrm{y}\right)\rightarrow\left(\mathrm{0},\mathrm{0}\right)} {\mathrm{lim}ln}\left(\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} }\right) \\ $$$$\:\:=\underset{\left(\mathrm{r},\theta\right)\rightarrow\left(\mathrm{0},\mathrm{0}\right)} {\mathrm{lim}ln}\left(\frac{\mathrm{r}^{\mathrm{2}} }{\mathrm{r}^{\mathrm{2}} \left(\mathrm{cos}^{\mathrm{2}} \theta−\mathrm{sin}^{\mathrm{2}} \theta\right)}\right) \\ $$$$\:\:=\underset{\left(\mathrm{r},\theta\right)\rightarrow\left(\mathrm{0},\mathrm{0}\right)} {\mathrm{lim}ln}\left(\frac{\mathrm{1}}{\mathrm{cos2}\theta}\right)=\mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{1}}\right)=\mathrm{0} \\ $$
Commented by mohammad17 last updated on 28/Dec/20
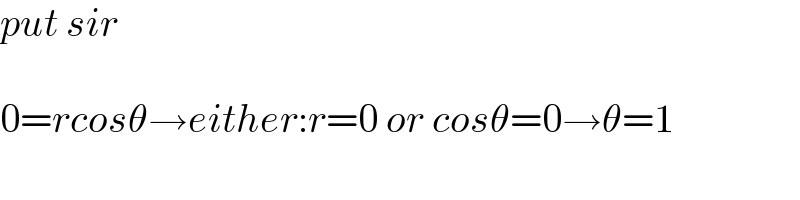
$${put}\:{sir}\: \\ $$$$ \\ $$$$\mathrm{0}={rcos}\theta\rightarrow{either}:{r}=\mathrm{0}\:{or}\:{cos}\theta=\mathrm{0}\rightarrow\theta=\mathrm{1} \\ $$
