
Question Number 127088 by MathSh last updated on 26/Dec/20
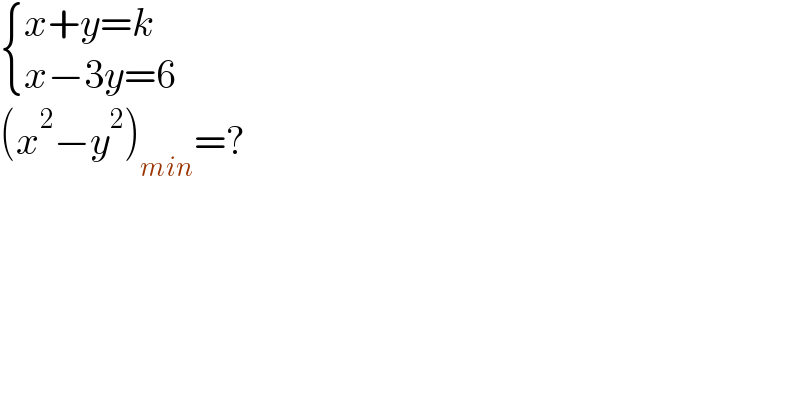
$$\begin{cases}{{x}+{y}={k}}\\{{x}−\mathrm{3}{y}=\mathrm{6}}\end{cases} \\ $$$$\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)_{{min}} =? \\ $$
Commented by hknkrc46 last updated on 26/Dec/20
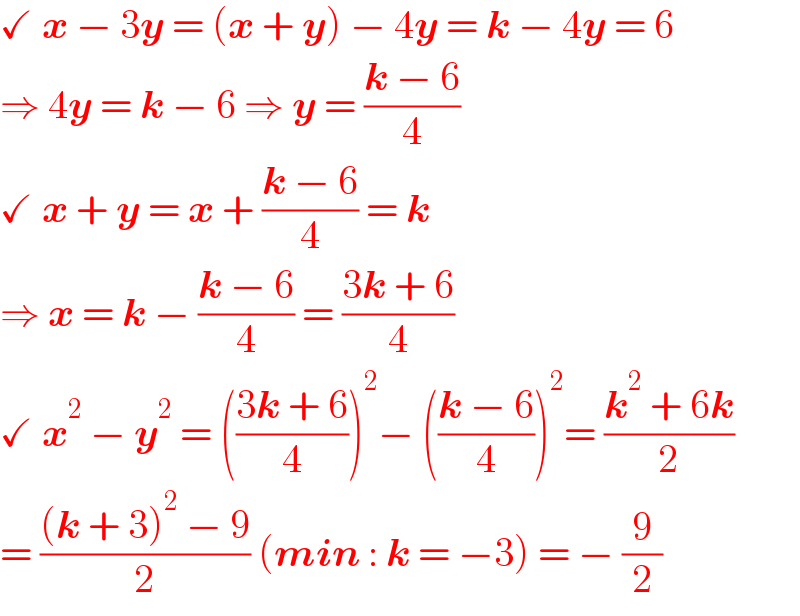
$$\checkmark\:\boldsymbol{{x}}\:−\:\mathrm{3}\boldsymbol{{y}}\:=\:\left(\boldsymbol{{x}}\:+\:\boldsymbol{{y}}\right)\:−\:\mathrm{4}\boldsymbol{{y}}\:=\:\boldsymbol{{k}}\:−\:\mathrm{4}\boldsymbol{{y}}\:=\:\mathrm{6} \\ $$$$\Rightarrow\:\mathrm{4}\boldsymbol{{y}}\:=\:\boldsymbol{{k}}\:−\:\mathrm{6}\:\Rightarrow\:\boldsymbol{{y}}\:=\:\frac{\boldsymbol{{k}}\:−\:\mathrm{6}}{\mathrm{4}} \\ $$$$\checkmark\:\boldsymbol{{x}}\:+\:\boldsymbol{{y}}\:=\:\boldsymbol{{x}}\:+\:\frac{\boldsymbol{{k}}\:−\:\mathrm{6}}{\mathrm{4}}\:=\:\boldsymbol{{k}} \\ $$$$\Rightarrow\:\boldsymbol{{x}}\:=\:\boldsymbol{{k}}\:−\:\frac{\boldsymbol{{k}}\:−\:\mathrm{6}}{\mathrm{4}}\:=\:\frac{\mathrm{3}\boldsymbol{{k}}\:+\:\mathrm{6}}{\mathrm{4}} \\ $$$$\checkmark\:\boldsymbol{{x}}^{\mathrm{2}} \:−\:\boldsymbol{{y}}^{\mathrm{2}} \:=\:\left(\frac{\mathrm{3}\boldsymbol{{k}}\:+\:\mathrm{6}}{\mathrm{4}}\right)^{\mathrm{2}} −\:\left(\frac{\boldsymbol{{k}}\:−\:\mathrm{6}}{\mathrm{4}}\right)^{\mathrm{2}} =\:\frac{\boldsymbol{{k}}^{\mathrm{2}} \:+\:\mathrm{6}\boldsymbol{{k}}}{\mathrm{2}} \\ $$$$=\:\frac{\left(\boldsymbol{{k}}\:+\:\mathrm{3}\right)^{\mathrm{2}} \:−\:\mathrm{9}}{\mathrm{2}}\:\left(\boldsymbol{{min}}\::\:\boldsymbol{{k}}\:=\:−\mathrm{3}\right)\:=\:−\:\frac{\mathrm{9}}{\mathrm{2}} \\ $$
Commented by MathSh last updated on 27/Dec/20

$${Thanks}\:{sir} \\ $$
Answered by Olaf last updated on 26/Dec/20
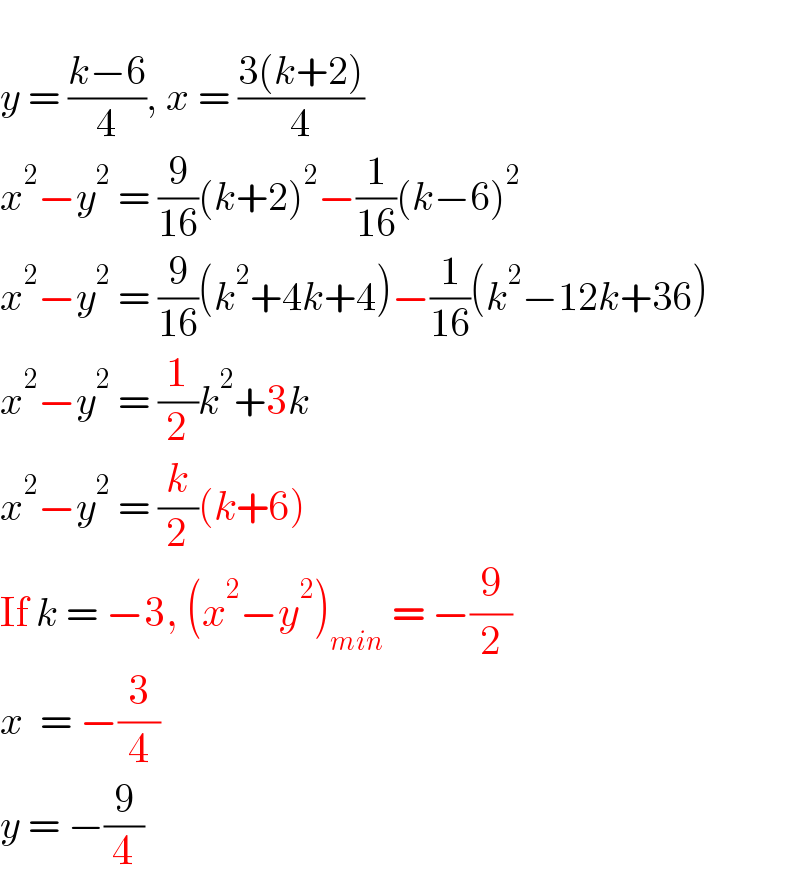
$$ \\ $$$${y}\:=\:\frac{{k}−\mathrm{6}}{\mathrm{4}},\:{x}\:=\:\frac{\mathrm{3}\left({k}+\mathrm{2}\right)}{\mathrm{4}} \\ $$$${x}^{\mathrm{2}} −{y}^{\mathrm{2}} \:=\:\frac{\mathrm{9}}{\mathrm{16}}\left({k}+\mathrm{2}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{16}}\left({k}−\mathrm{6}\right)^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} −{y}^{\mathrm{2}} \:=\:\frac{\mathrm{9}}{\mathrm{16}}\left({k}^{\mathrm{2}} +\mathrm{4}{k}+\mathrm{4}\right)−\frac{\mathrm{1}}{\mathrm{16}}\left({k}^{\mathrm{2}} −\mathrm{12}{k}+\mathrm{36}\right) \\ $$$${x}^{\mathrm{2}} −{y}^{\mathrm{2}} \:=\:\frac{\mathrm{1}}{\mathrm{2}}{k}^{\mathrm{2}} +\mathrm{3}{k} \\ $$$${x}^{\mathrm{2}} −{y}^{\mathrm{2}} \:=\:\frac{{k}}{\mathrm{2}}\left({k}+\mathrm{6}\right) \\ $$$$\mathrm{If}\:{k}\:=\:−\mathrm{3},\:\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)_{{min}} \:=\:−\frac{\mathrm{9}}{\mathrm{2}} \\ $$$${x}\:\:=\:−\frac{\mathrm{3}}{\mathrm{4}} \\ $$$${y}\:=\:−\frac{\mathrm{9}}{\mathrm{4}} \\ $$
Commented by MathSh last updated on 27/Dec/20

$${Thanks}\:{sir} \\ $$
Answered by Olaf last updated on 26/Dec/20
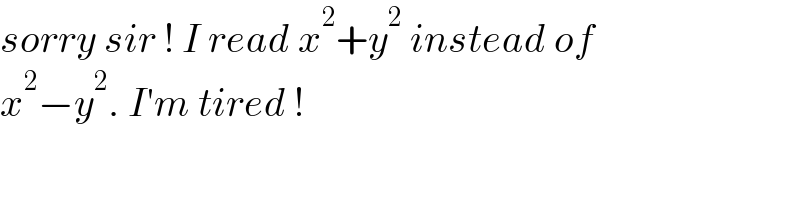
$${sorry}\:{sir}\:!\:{I}\:{read}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \:{instead}\:{of} \\ $$$${x}^{\mathrm{2}} −{y}^{\mathrm{2}} .\:{I}'{m}\:{tired}\:! \\ $$
Commented by MathSh last updated on 27/Dec/20

$${Yes},\:{thanks}\:{sir} \\ $$
Answered by mathmax by abdo last updated on 26/Dec/20
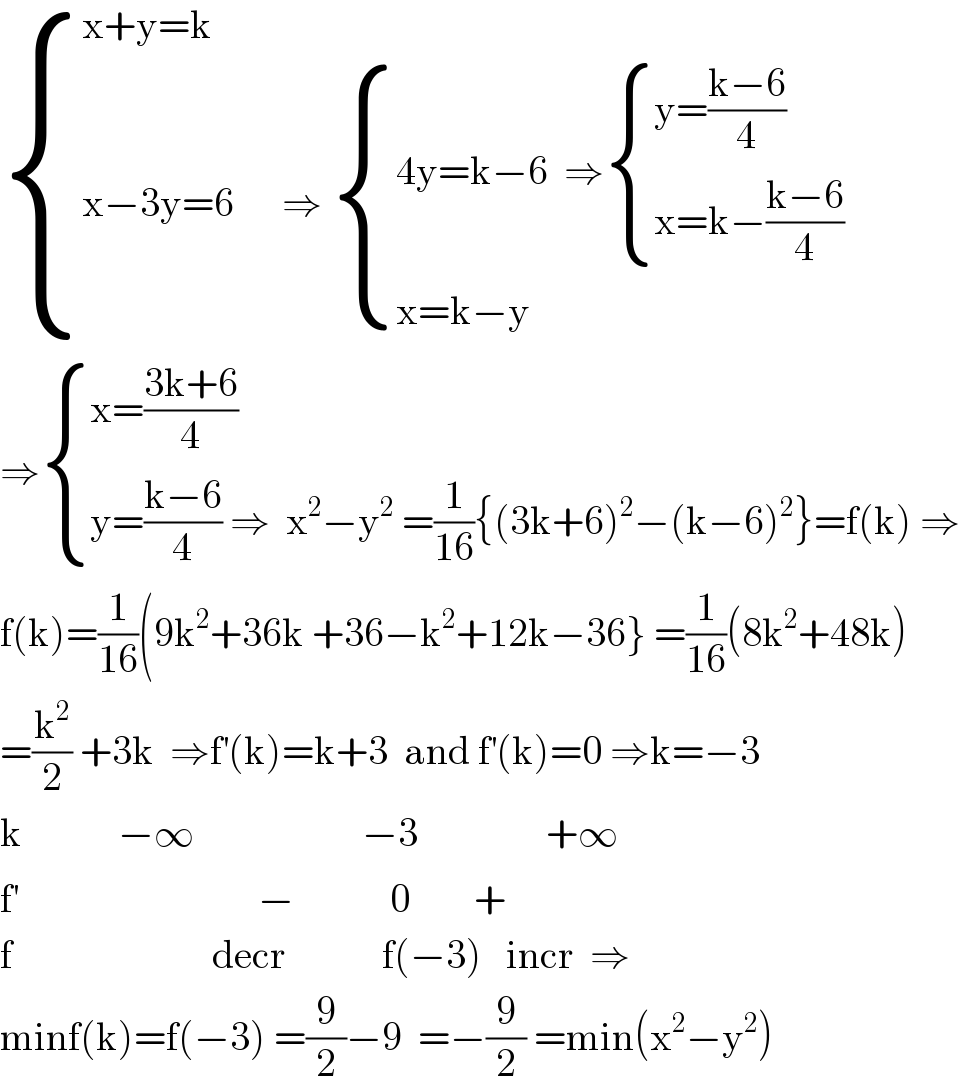
$$\begin{cases}{\mathrm{x}+\mathrm{y}=\mathrm{k}}\\{\mathrm{x}−\mathrm{3y}=\mathrm{6}\:\:\:\:\:\:\Rightarrow\:\begin{cases}{\mathrm{4y}=\mathrm{k}−\mathrm{6}\:\:\Rightarrow\begin{cases}{\mathrm{y}=\frac{\mathrm{k}−\mathrm{6}}{\mathrm{4}}}\\{\mathrm{x}=\mathrm{k}−\frac{\mathrm{k}−\mathrm{6}}{\mathrm{4}}}\end{cases}}\\{\mathrm{x}=\mathrm{k}−\mathrm{y}}\end{cases}}\end{cases} \\ $$$$\Rightarrow\begin{cases}{\mathrm{x}=\frac{\mathrm{3k}+\mathrm{6}}{\mathrm{4}}}\\{\mathrm{y}=\frac{\mathrm{k}−\mathrm{6}}{\mathrm{4}}\:\Rightarrow\:\:\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} \:=\frac{\mathrm{1}}{\mathrm{16}}\left\{\left(\mathrm{3k}+\mathrm{6}\right)^{\mathrm{2}} −\left(\mathrm{k}−\mathrm{6}\right)^{\mathrm{2}} \right\}=\mathrm{f}\left(\mathrm{k}\right)\:\Rightarrow}\end{cases} \\ $$$$\mathrm{f}\left(\mathrm{k}\right)=\frac{\mathrm{1}}{\mathrm{16}}\left(\mathrm{9k}^{\mathrm{2}} +\mathrm{36k}\:+\mathrm{36}−\mathrm{k}^{\mathrm{2}} +\mathrm{12k}−\mathrm{36}\right\}\:=\frac{\mathrm{1}}{\mathrm{16}}\left(\mathrm{8k}^{\mathrm{2}} +\mathrm{48k}\right) \\ $$$$=\frac{\mathrm{k}^{\mathrm{2}} }{\mathrm{2}}\:+\mathrm{3k}\:\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{k}\right)=\mathrm{k}+\mathrm{3}\:\:\mathrm{and}\:\mathrm{f}^{'} \left(\mathrm{k}\right)=\mathrm{0}\:\Rightarrow\mathrm{k}=−\mathrm{3} \\ $$$$\mathrm{k}\:\:\:\:\:\:\:\:\:\:\:\:−\infty\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{3}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\infty \\ $$$$\mathrm{f}^{'} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:+ \\ $$$$\mathrm{f}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{decr}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{f}\left(−\mathrm{3}\right)\:\:\:\mathrm{incr}\:\:\Rightarrow \\ $$$$\mathrm{minf}\left(\mathrm{k}\right)=\mathrm{f}\left(−\mathrm{3}\right)\:=\frac{\mathrm{9}}{\mathrm{2}}−\mathrm{9}\:\:=−\frac{\mathrm{9}}{\mathrm{2}}\:=\mathrm{min}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} \right) \\ $$
Commented by MathSh last updated on 27/Dec/20

$${Thanks}\:{sir} \\ $$
