Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 127085 by mnjuly1970 last updated on 26/Dec/20

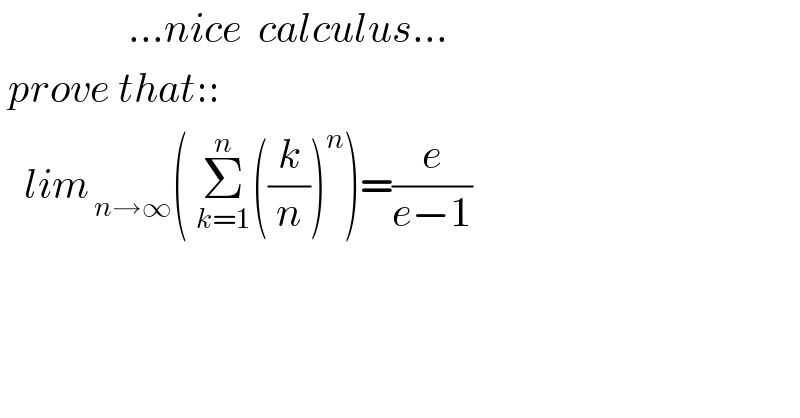
...nice calculus... prove that:: lim_( n→∞) ( Σ_(k=1) ^n ((k/n))^n )=(e/(e−1))

$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:...{nice}\:\:{calculus}... \\ $$$$\:{prove}\:{that}:: \\ $$$$\:\:\:{lim}_{\:{n}\rightarrow\infty} \left(\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\frac{{k}}{{n}}\right)^{{n}} \right)=\frac{{e}}{{e}−\mathrm{1}} \\ $$$$ \\ $$

Commented by mnjuly1970 last updated on 27/Dec/20

thanks alot...

$$\:\:\:\:{thanks}\:\:{alot}... \\ $$

Answered by mindispower last updated on 27/Dec/20

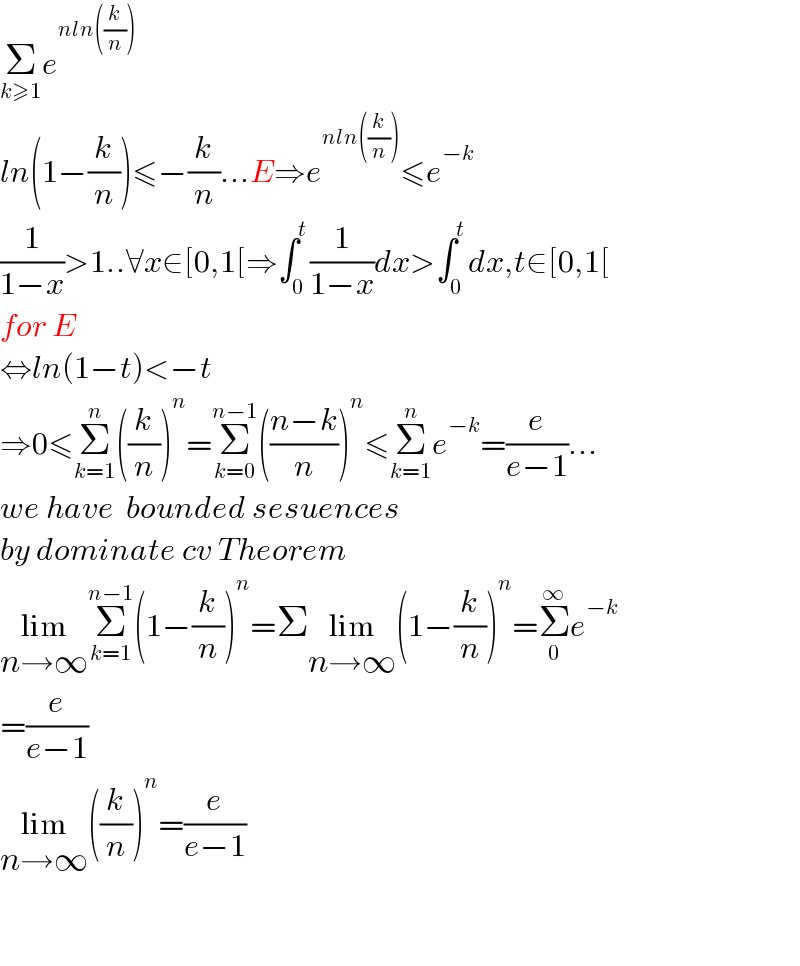
Σ_(k≥1) e^(nln((k/n))) ln(1−(k/n))≤−(k/n)...E⇒e^(nln((k/n))) ≤e^(−k) (1/(1−x))>1..∀x∈[0,1[⇒∫_0 ^t (1/(1−x))dx>∫_0 ^t dx,t∈[0,1[ for E ⇔ln(1−t)<−t ⇒0≤Σ_(k=1) ^n ((k/n))^n =Σ_(k=0) ^(n−1) (((n−k)/n))^n ≤Σ_(k=1) ^n e^(−k) =(e/(e−1))... we have bounded sesuences by dominate cv Theorem lim_(n→∞) Σ_(k=1) ^(n−1) (1−(k/n))^n =Σlim_(n→∞) (1−(k/n))^n =Σ_0 ^∞ e^(−k) =(e/(e−1)) lim_(n→∞) ((k/n))^n =(e/(e−1))

$$\underset{{k}\geqslant\mathrm{1}} {\sum}{e}^{{nln}\left(\frac{{k}}{{n}}\right)} \\ $$$${ln}\left(\mathrm{1}−\frac{{k}}{{n}}\right)\leqslant−\frac{{k}}{{n}}...{E}\Rightarrow{e}^{{nln}\left(\frac{{k}}{{n}}\right)} \leqslant{e}^{−{k}} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}−{x}}>\mathrm{1}..\forall{x}\in\left[\mathrm{0},\mathrm{1}\left[\Rightarrow\int_{\mathrm{0}} ^{{t}} \frac{\mathrm{1}}{\mathrm{1}−{x}}{dx}>\int_{\mathrm{0}} ^{{t}} {dx},{t}\in\left[\mathrm{0},\mathrm{1}\left[\right.\right.\right.\right. \\ $$$${for}\:{E}\: \\ $$$$\Leftrightarrow{ln}\left(\mathrm{1}−{t}\right)<−{t} \\ $$$$\Rightarrow\mathrm{0}\leqslant\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\frac{{k}}{{n}}\right)^{{n}} =\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\left(\frac{{n}−{k}}{{n}}\right)^{{n}} \leqslant\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{e}^{−{k}} =\frac{{e}}{{e}−\mathrm{1}}... \\ $$$${we}\:{have}\:\:{bounded}\:{sesuences} \\ $$$${by}\:{dominate}\:{cv}\:{Theorem}\: \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}\left(\mathrm{1}−\frac{{k}}{{n}}\right)^{{n}} =\Sigma\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}−\frac{{k}}{{n}}\right)^{{n}} =\underset{\mathrm{0}} {\overset{\infty} {\sum}}{e}^{−{k}} \\ $$$$=\frac{{e}}{{e}−\mathrm{1}} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{{k}}{{n}}\right)^{{n}} =\frac{{e}}{{e}−\mathrm{1}} \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com