
Previous in Differential Equation Next in Differential Equation
Question Number 126896 by BHOOPENDRA last updated on 25/Dec/20

$${yy}''−\left({y}'\right)^{\mathrm{2}} ={e}^{{ax}\:} {find}\:{genral}\:{solution}? \\ $$
Commented by liberty last updated on 25/Dec/20
![ok i try solve it. for equation yy′′−(y′)^2 =e^(ax) or y′′−(((y′)^2 )/y) = (e^(ax) /y) put y′=v(y) ; where y=f(x) then y′′ = v(y)v′(y). the equation becomes v′−(v/y) = (e^(ax) /y). the term e^(ax) can be considered as a constant. The integrating factor is (1/y) and the solution given by v=y[ ∫ (e^(ax) /y^2 ) dy + b ] v = by−e^(ax) ; give (dy/dx) −by = −e^(ax) for this equation integrating factor is e^(−bx) and the solution is y = e^(bx) [ ∫ (e^(−ax) )(e^(−bx) )dx + c ] y= (e^(ax) /(b−a)) +c.e^(bx) , b≠a](Q126908.png)
$${ok}\:{i}\:{try}\:{solve}\:{it}. \\ $$$$ \\ $$$${for}\:{equation}\:{yy}''−\left({y}'\right)^{\mathrm{2}} ={e}^{{ax}} \\ $$$$\:{or}\:{y}''−\frac{\left({y}'\right)^{\mathrm{2}} }{{y}}\:=\:\frac{{e}^{{ax}} }{{y}} \\ $$$${put}\:{y}'={v}\left({y}\right)\:;\:{where}\:{y}={f}\left({x}\right) \\ $$$${then}\:{y}''\:=\:{v}\left({y}\right){v}'\left({y}\right).\:{the}\:{equation}\:{becomes} \\ $$$$\:{v}'−\frac{{v}}{{y}}\:=\:\frac{{e}^{{ax}} }{{y}}.\:\:{the}\:{term}\:{e}^{{ax}} \:{can}\:{be}\:{considered} \\ $$$${as}\:{a}\:{constant}.\:{The}\:{integrating}\:{factor}\:{is}\:\frac{\mathrm{1}}{{y}} \\ $$$${and}\:{the}\:{solution}\:{given}\:{by}\: \\ $$$${v}={y}\left[\:\int\:\frac{{e}^{{ax}} }{{y}^{\mathrm{2}} }\:{dy}\:+\:{b}\:\right]\: \\ $$$${v}\:=\:{by}−{e}^{{ax}} \:;\:{give}\:\frac{{dy}}{{dx}}\:−{by}\:=\:−{e}^{{ax}} \\ $$$$\:{for}\:{this}\:{equation}\:{integrating}\:{factor} \\ $$$${is}\:{e}^{−{bx}} \:{and}\:{the}\:{solution}\:{is} \\ $$$${y}\:=\:{e}^{{bx}} \:\left[\:\int\:\left({e}^{−{ax}} \right)\left({e}^{−{bx}} \right){dx}\:+\:{c}\:\right] \\ $$$${y}=\:\frac{{e}^{{ax}} }{{b}−{a}}\:+{c}.{e}^{{bx}} \:,\:{b}\neq{a}\:\: \\ $$$$ \\ $$
Commented by mr W last updated on 25/Dec/20
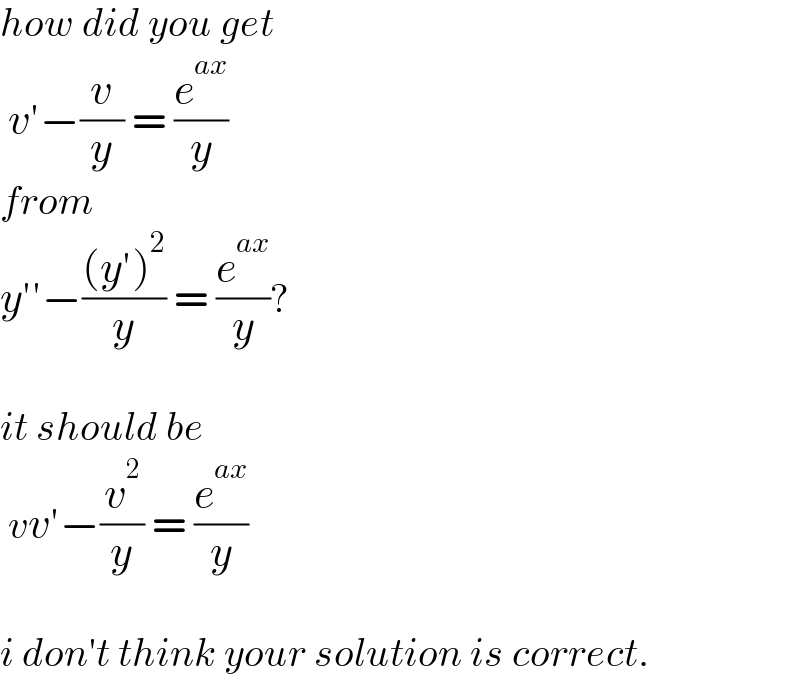
$${how}\:{did}\:{you}\:{get} \\ $$$$\:{v}'−\frac{{v}}{{y}}\:=\:\frac{{e}^{{ax}} }{{y}} \\ $$$${from} \\ $$$${y}''−\frac{\left({y}'\right)^{\mathrm{2}} }{{y}}\:=\:\frac{{e}^{{ax}} }{{y}}? \\ $$$$ \\ $$$${it}\:{should}\:{be} \\ $$$$\:{vv}'−\frac{{v}^{\mathrm{2}} }{{y}}\:=\:\frac{{e}^{{ax}} }{{y}} \\ $$$$ \\ $$$${i}\:{don}'{t}\:{think}\:{your}\:{solution}\:{is}\:{correct}. \\ $$
