
Question Number 126765 by mnjuly1970 last updated on 24/Dec/20
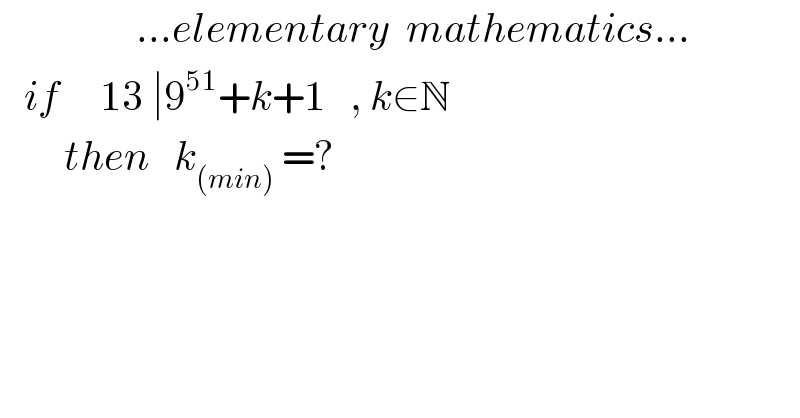
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:...{elementary}\:\:{mathematics}... \\ $$$$\:\:\:{if}\:\:\:\:\:\mathrm{13}\:\mid\mathrm{9}^{\mathrm{51}} +{k}+\mathrm{1}\:\:\:,\:{k}\in\mathbb{N} \\ $$$$\:\:\:\:\:\:\:\:{then}\:\:\:{k}_{\left({min}\right)} \:=? \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\: \\ $$
Answered by floor(10²Eta[1]) last updated on 24/Dec/20
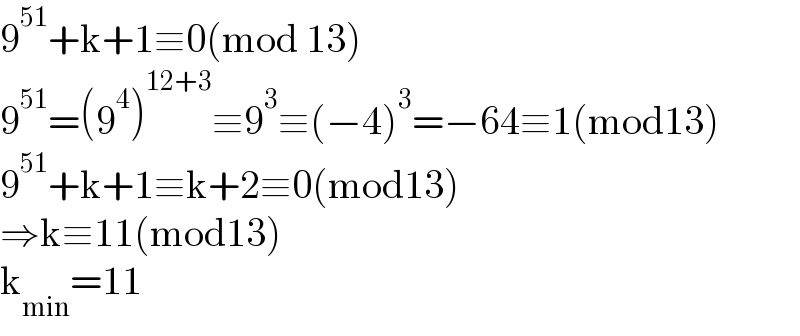
$$\mathrm{9}^{\mathrm{51}} +\mathrm{k}+\mathrm{1}\equiv\mathrm{0}\left(\mathrm{mod}\:\mathrm{13}\right) \\ $$$$\mathrm{9}^{\mathrm{51}} =\left(\mathrm{9}^{\mathrm{4}} \right)^{\mathrm{12}+\mathrm{3}} \equiv\mathrm{9}^{\mathrm{3}} \equiv\left(−\mathrm{4}\right)^{\mathrm{3}} =−\mathrm{64}\equiv\mathrm{1}\left(\mathrm{mod13}\right) \\ $$$$\mathrm{9}^{\mathrm{51}} +\mathrm{k}+\mathrm{1}\equiv\mathrm{k}+\mathrm{2}\equiv\mathrm{0}\left(\mathrm{mod13}\right) \\ $$$$\Rightarrow\mathrm{k}\equiv\mathrm{11}\left(\mathrm{mod13}\right) \\ $$$$\mathrm{k}_{\mathrm{min}} =\mathrm{11} \\ $$
Commented by mnjuly1970 last updated on 24/Dec/20

$${grateful}.. \\ $$
Commented by JDamian last updated on 25/Dec/20
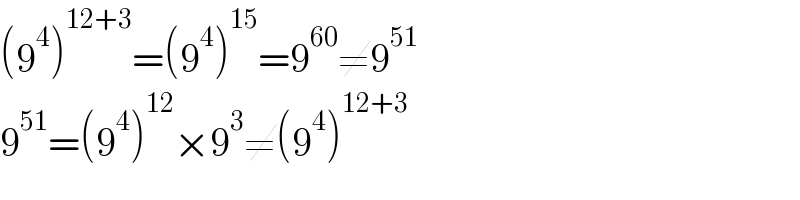
$$\left(\mathrm{9}^{\mathrm{4}} \right)^{\mathrm{12}+\mathrm{3}} =\left(\mathrm{9}^{\mathrm{4}} \right)^{\mathrm{15}} =\mathrm{9}^{\mathrm{60}} \neq\mathrm{9}^{\mathrm{51}} \\ $$$$\mathrm{9}^{\mathrm{51}} =\left(\mathrm{9}^{\mathrm{4}} \right)^{\mathrm{12}} ×\mathrm{9}^{\mathrm{3}} \neq\left(\mathrm{9}^{\mathrm{4}} \right)^{\mathrm{12}+\mathrm{3}} \\ $$
Commented by floor(10²Eta[1]) last updated on 25/Dec/20
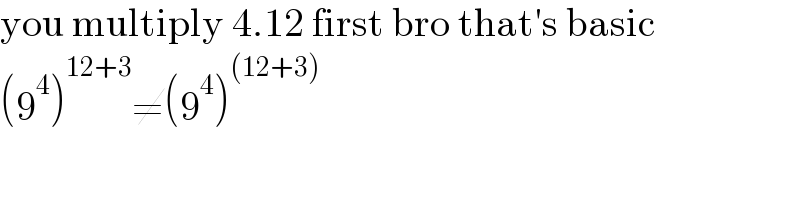
$$\mathrm{you}\:\mathrm{multiply}\:\mathrm{4}.\mathrm{12}\:\mathrm{first}\:\mathrm{bro}\:\mathrm{that}'\mathrm{s}\:\mathrm{basic} \\ $$$$\left(\mathrm{9}^{\mathrm{4}} \right)^{\mathrm{12}+\mathrm{3}} \neq\left(\mathrm{9}^{\mathrm{4}} \right)^{\left(\mathrm{12}+\mathrm{3}\right)} \\ $$$$ \\ $$
