
Question Number 126619 by O Predador last updated on 22/Dec/20
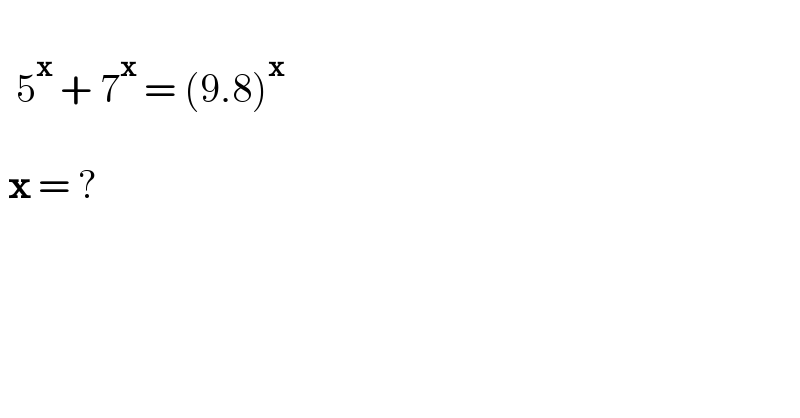
$$\: \\ $$$$\:\:\mathrm{5}^{\boldsymbol{\mathrm{x}}} \:+\:\mathrm{7}^{\boldsymbol{\mathrm{x}}} \:=\:\left(\mathrm{9}.\mathrm{8}\right)^{\boldsymbol{\mathrm{x}}} \\ $$$$\: \\ $$$$\:\boldsymbol{\mathrm{x}}\:=\:? \\ $$$$\: \\ $$
Answered by Dwaipayan Shikari last updated on 22/Dec/20
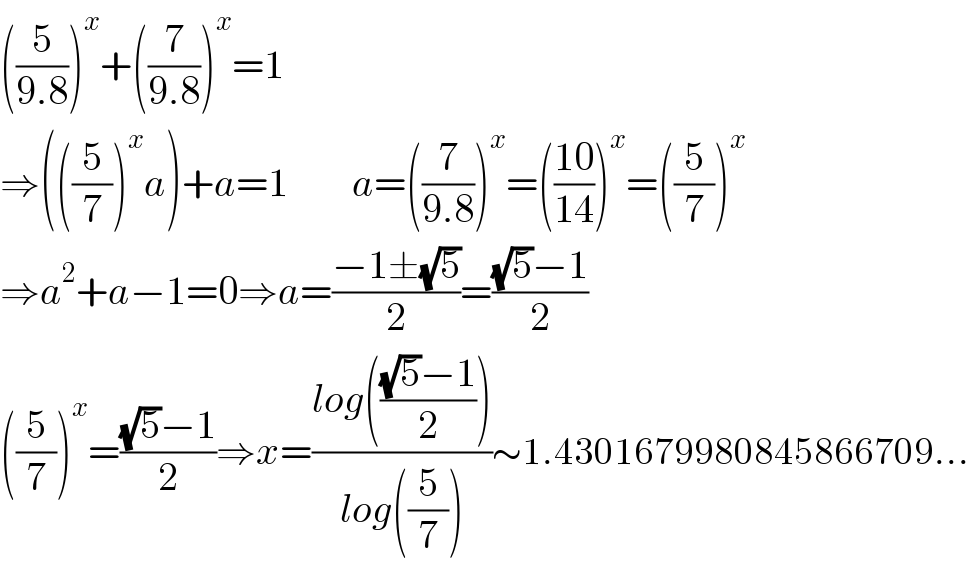
$$\left(\frac{\mathrm{5}}{\mathrm{9}.\mathrm{8}}\right)^{{x}} +\left(\frac{\mathrm{7}}{\mathrm{9}.\mathrm{8}}\right)^{{x}} =\mathrm{1} \\ $$$$\Rightarrow\left(\left(\frac{\mathrm{5}}{\mathrm{7}}\right)^{{x}} {a}\right)+{a}=\mathrm{1}\:\:\:\:\:\:\:\:{a}=\left(\frac{\mathrm{7}}{\mathrm{9}.\mathrm{8}}\right)^{{x}} =\left(\frac{\mathrm{10}}{\mathrm{14}}\right)^{{x}} =\left(\frac{\mathrm{5}}{\mathrm{7}}\right)^{{x}} \\ $$$$\Rightarrow{a}^{\mathrm{2}} +{a}−\mathrm{1}=\mathrm{0}\Rightarrow{a}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}}=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}} \\ $$$$\left(\frac{\mathrm{5}}{\mathrm{7}}\right)^{{x}} =\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}\Rightarrow{x}=\frac{{log}\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}\right)}{{log}\left(\frac{\mathrm{5}}{\mathrm{7}}\right)}\sim\mathrm{1}.\mathrm{4301679980845866709}... \\ $$
Commented by O Predador last updated on 22/Dec/20

$${Wonderful}! \\ $$
Answered by Olaf last updated on 22/Dec/20
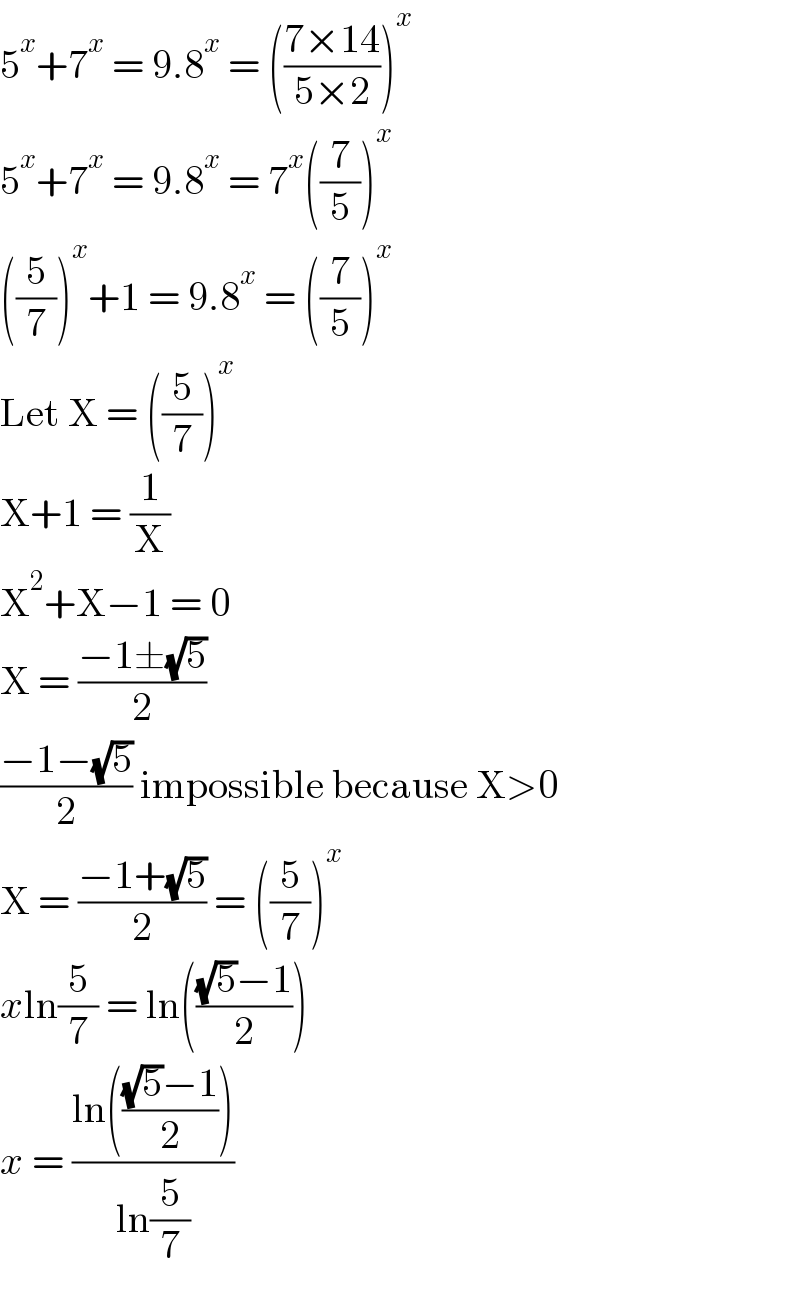
$$\mathrm{5}^{{x}} +\mathrm{7}^{{x}} \:=\:\mathrm{9}.\mathrm{8}^{{x}} \:=\:\left(\frac{\mathrm{7}×\mathrm{14}}{\mathrm{5}×\mathrm{2}}\right)^{{x}} \\ $$$$\mathrm{5}^{{x}} +\mathrm{7}^{{x}} \:=\:\mathrm{9}.\mathrm{8}^{{x}} \:=\:\mathrm{7}^{{x}} \left(\frac{\mathrm{7}}{\mathrm{5}}\right)^{{x}} \\ $$$$\left(\frac{\mathrm{5}}{\mathrm{7}}\right)^{{x}} +\mathrm{1}\:=\:\mathrm{9}.\mathrm{8}^{{x}} \:=\:\left(\frac{\mathrm{7}}{\mathrm{5}}\right)^{{x}} \\ $$$$\mathrm{Let}\:\mathrm{X}\:=\:\left(\frac{\mathrm{5}}{\mathrm{7}}\right)^{{x}} \\ $$$$\mathrm{X}+\mathrm{1}\:=\:\frac{\mathrm{1}}{\mathrm{X}} \\ $$$$\mathrm{X}^{\mathrm{2}} +\mathrm{X}−\mathrm{1}\:=\:\mathrm{0} \\ $$$$\mathrm{X}\:=\:\frac{−\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\frac{−\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\:\mathrm{impossible}\:\mathrm{because}\:\mathrm{X}>\mathrm{0} \\ $$$$\mathrm{X}\:=\:\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:=\:\left(\frac{\mathrm{5}}{\mathrm{7}}\right)^{{x}} \\ $$$${x}\mathrm{ln}\frac{\mathrm{5}}{\mathrm{7}}\:=\:\mathrm{ln}\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}\right) \\ $$$${x}\:=\:\frac{\mathrm{ln}\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{ln}\frac{\mathrm{5}}{\mathrm{7}}} \\ $$
