
Question Number 126507 by joki last updated on 21/Dec/20
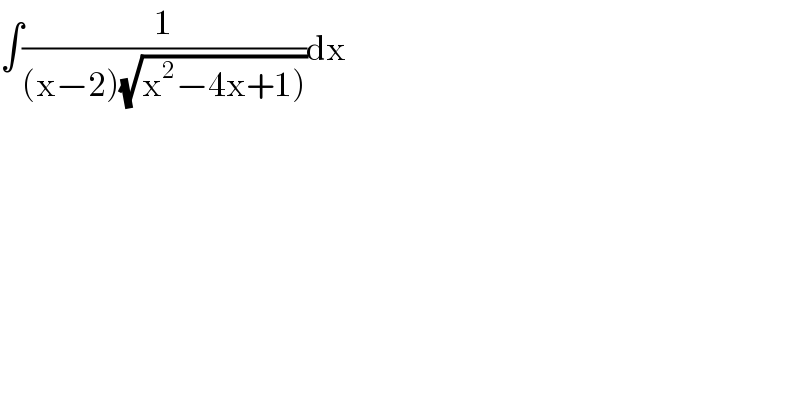
$$\int\frac{\mathrm{1}}{\left(\mathrm{x}−\mathrm{2}\right)\sqrt{\left.\mathrm{x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{1}\right)}}\mathrm{dx} \\ $$
Answered by Dwaipayan Shikari last updated on 21/Dec/20
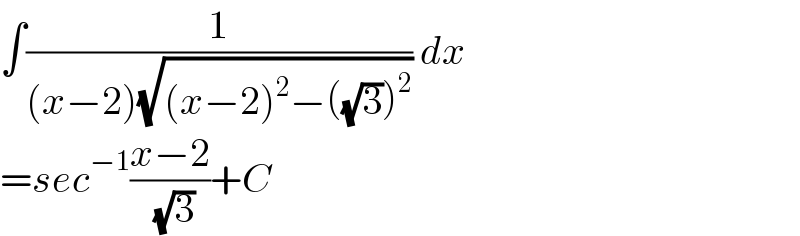
$$\int\frac{\mathrm{1}}{\left({x}−\mathrm{2}\right)\sqrt{\left({x}−\mathrm{2}\right)^{\mathrm{2}} −\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }}\:{dx} \\ $$$$={sec}^{−\mathrm{1}} \frac{{x}−\mathrm{2}}{\:\sqrt{\mathrm{3}}}+{C} \\ $$
Commented by joki last updated on 21/Dec/20

$$\mathrm{can}\:\mathrm{you}\:\mathrm{detail}\:\mathrm{your}\:\mathrm{answer}\:\mathrm{sir}.\mathrm{thanks} \\ $$
Answered by Ar Brandon last updated on 21/Dec/20
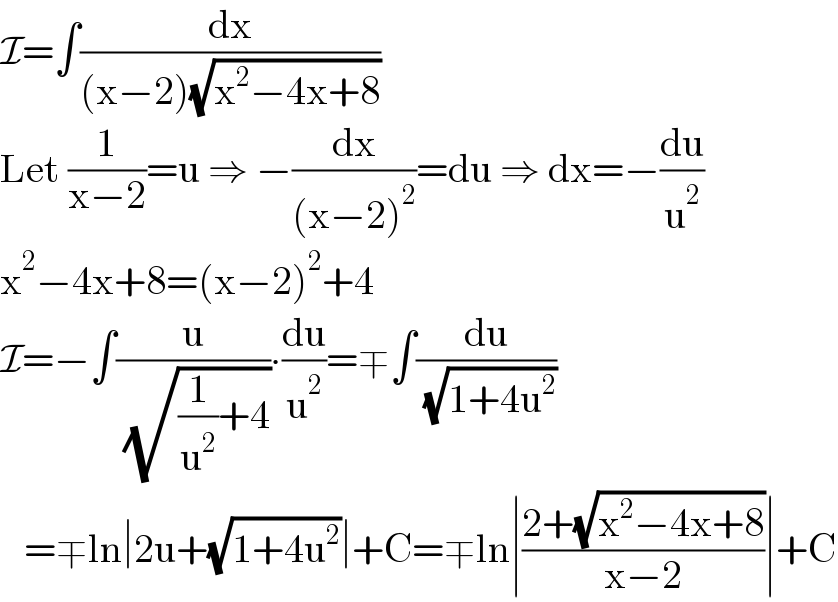
$$\mathcal{I}=\int\frac{\mathrm{dx}}{\left(\mathrm{x}−\mathrm{2}\right)\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{8}}} \\ $$$$\mathrm{Let}\:\frac{\mathrm{1}}{\mathrm{x}−\mathrm{2}}=\mathrm{u}\:\Rightarrow\:−\frac{\mathrm{dx}}{\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} }=\mathrm{du}\:\Rightarrow\:\mathrm{dx}=−\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} } \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{8}=\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} +\mathrm{4} \\ $$$$\mathcal{I}=−\int\frac{\mathrm{u}}{\:\sqrt{\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} }+\mathrm{4}}}\centerdot\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} }=\mp\int\frac{\mathrm{du}}{\:\sqrt{\mathrm{1}+\mathrm{4u}^{\mathrm{2}} }} \\ $$$$\:\:\:=\mp\mathrm{ln}\mid\mathrm{2u}+\sqrt{\mathrm{1}+\mathrm{4u}^{\mathrm{2}} }\mid+\mathrm{C}=\mp\mathrm{ln}\mid\frac{\mathrm{2}+\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{8}}}{\mathrm{x}−\mathrm{2}}\mid+\mathrm{C} \\ $$
Answered by Ar Brandon last updated on 21/Dec/20

$$\mathcal{I}=\int\frac{\mathrm{dx}}{\left(\mathrm{x}−\mathrm{2}\right)\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{1}}} \\ $$$$\mathrm{Let}\:\frac{\mathrm{1}}{\mathrm{x}−\mathrm{2}}=\mathrm{u}\:\Rightarrow\:−\frac{\mathrm{dx}}{\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} }=\mathrm{du}\:\Rightarrow\:\mathrm{dx}=−\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} } \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{1}=\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} −\mathrm{3} \\ $$$$\mathcal{I}=−\int\frac{\mathrm{u}}{\:\sqrt{\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} }−\mathrm{3}}}\centerdot\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} }=\mp\int\frac{\mathrm{du}}{\:\sqrt{\mathrm{1}−\mathrm{3u}^{\mathrm{2}} }} \\ $$$$\:\:\:=\mp\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\mathrm{Arcsin}\left(\sqrt{\mathrm{3}}\mathrm{u}\right)+\mathrm{C}=\mp\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\mathrm{Arcsin}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{x}−\mathrm{2}}\right)+\mathrm{C} \\ $$
Answered by MJS_new last updated on 21/Dec/20
![∫(dx/((x−2)(√(x^2 −4x+1))))= [t=((x−2+(√(x^2 −4x+1)))/( (√3))) → dx=((√(3(x^2 −4x+1))/(x−2+(√(x^2 −4x+1))))] =(2/( (√3)))∫(dt/(t^2 +1))=(2/( (√3)))arctan t = =(2/( (√3)))arctan ((x−2+(√(x^2 −4x+1)))/( (√3))) +C](Q126533.png)
$$\int\frac{{dx}}{\left({x}−\mathrm{2}\right)\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{1}}}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{{x}−\mathrm{2}+\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{1}}}{\:\sqrt{\mathrm{3}}}\:\rightarrow\:{dx}=\frac{\sqrt{\mathrm{3}\left({x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{1}\right.}}{{x}−\mathrm{2}+\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{1}}}\right] \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\mathrm{arctan}\:{t}\:= \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\mathrm{arctan}\:\frac{{x}−\mathrm{2}+\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{1}}}{\:\sqrt{\mathrm{3}}}\:+{C} \\ $$
