
Question Number 126484 by Mathgreat last updated on 20/Dec/20
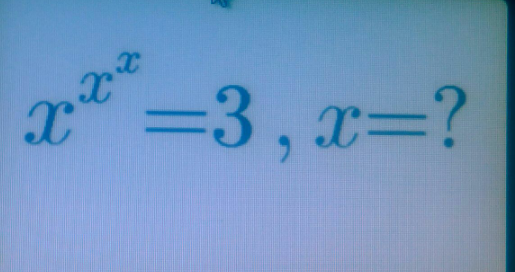
Commented by MJS_new last updated on 20/Dec/20

$$\approx\mathrm{1}.\mathrm{63507847} \\ $$
Commented by Mathgreat last updated on 20/Dec/20

$${yechim}. \\ $$$$ \\ $$
Commented by Mathgreat last updated on 20/Dec/20

$${prove} \\ $$
Commented by MJS_new last updated on 20/Dec/20

$$\mathrm{just}\:\mathrm{use}\:\mathrm{a}\:\mathrm{calculator} \\ $$$${f}\left({x}\right)={x}^{{x}^{{x}} } −\mathrm{3} \\ $$$${f}\left(\mathrm{1}\right)=−\mathrm{2} \\ $$$${f}\left(\mathrm{2}\right)=\mathrm{16} \\ $$$$\Rightarrow\:\mathrm{1}<{x}<\mathrm{2} \\ $$$${f}\left(\mathrm{1}.\mathrm{5}\right)\approx−.\mathrm{89} \\ $$$$\Rightarrow\:\mathrm{1}.\mathrm{5}<{x}<\mathrm{2} \\ $$$${f}\left(\mathrm{1}.\mathrm{6}\right)\approx−.\mathrm{29} \\ $$$$\Rightarrow\:\mathrm{1}.\mathrm{6}<{x}<\mathrm{2} \\ $$$${f}\left(\mathrm{1}.\mathrm{7}\right)\approx.\mathrm{70} \\ $$$$\Rightarrow\:\mathrm{1}.\mathrm{6}<{x}<\mathrm{1}.\mathrm{7} \\ $$$$... \\ $$
Commented by MJS_new last updated on 20/Dec/20
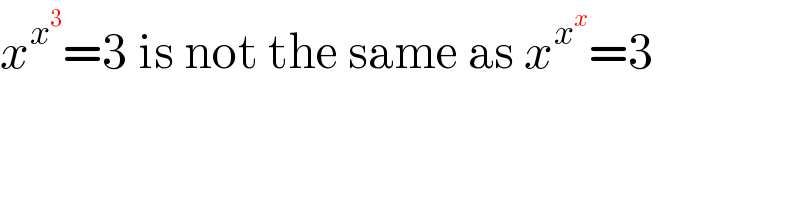
$${x}^{{x}^{\mathrm{3}} } =\mathrm{3}\:\mathrm{is}\:\mathrm{not}\:\mathrm{the}\:\mathrm{same}\:\mathrm{as}\:{x}^{{x}^{{x}} } =\mathrm{3} \\ $$
Commented by MathSh last updated on 20/Dec/20
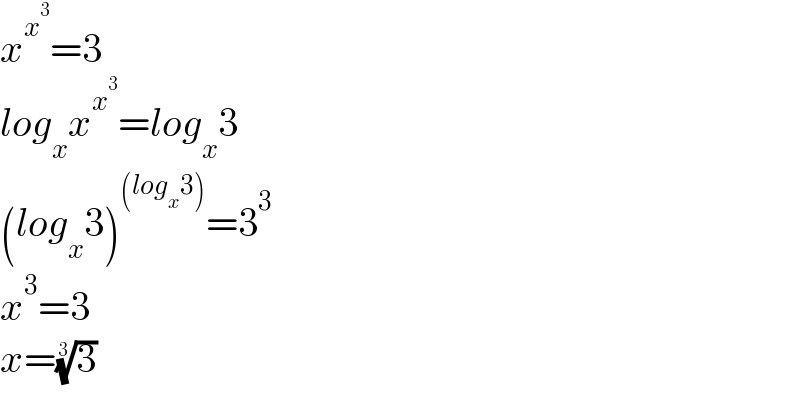
$${x}^{{x}^{\mathrm{3}} } =\mathrm{3} \\ $$$${log}_{{x}} {x}^{{x}^{\mathrm{3}} } ={log}_{{x}} \mathrm{3} \\ $$$$\left({log}_{{x}} \mathrm{3}\right)^{\left({log}_{{x}} \mathrm{3}\right)} =\mathrm{3}^{\mathrm{3}} \\ $$$${x}^{\mathrm{3}} =\mathrm{3} \\ $$$${x}=\sqrt[{\mathrm{3}}]{\mathrm{3}} \\ $$
