
Question Number 126389 by shaker last updated on 20/Dec/20
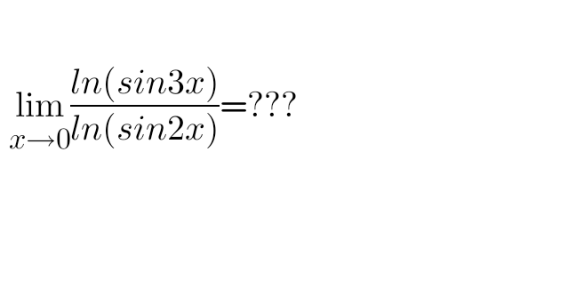
Answered by liberty last updated on 20/Dec/20
![lim_(x→0) (( [((3cos 3x)/(sin 3x))])/( [((2cos 2x)/(sin 2x))])) = lim_(x→0) ((3cos 3x)/(sin 3x))×((sin 2x)/(2cos 2x)) = (3/2)×lim_(x→0) ((sin 2x)/(sin 3x)) = 1](Q126393.png)
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\:\left[\frac{\mathrm{3cos}\:\mathrm{3}{x}}{\mathrm{sin}\:\mathrm{3}{x}}\right]}{\:\left[\frac{\mathrm{2cos}\:\mathrm{2}{x}}{\mathrm{sin}\:\mathrm{2}{x}}\right]}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{3cos}\:\mathrm{3}{x}}{\mathrm{sin}\:\mathrm{3}{x}}×\frac{\mathrm{sin}\:\mathrm{2}{x}}{\mathrm{2cos}\:\mathrm{2}{x}} \\ $$$$=\:\frac{\mathrm{3}}{\mathrm{2}}×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\mathrm{2}{x}}{\mathrm{sin}\:\mathrm{3}{x}}\:=\:\mathrm{1} \\ $$
Answered by mathmax by abdo last updated on 20/Dec/20
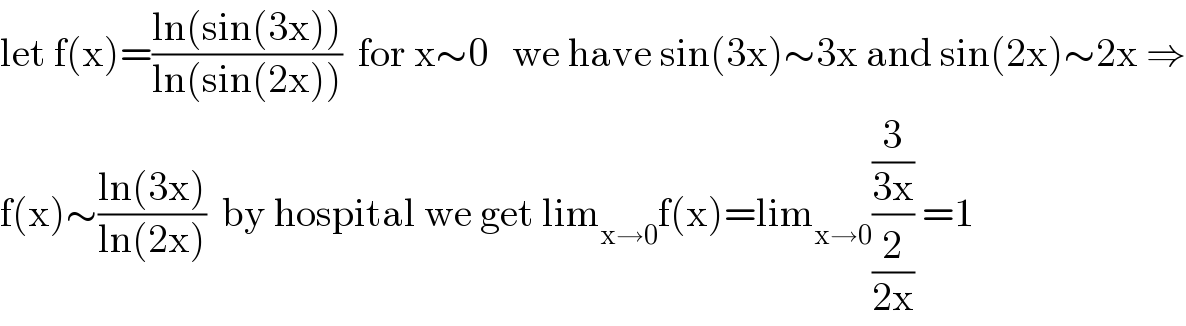
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{ln}\left(\mathrm{sin}\left(\mathrm{3x}\right)\right)}{\mathrm{ln}\left(\mathrm{sin}\left(\mathrm{2x}\right)\right)}\:\:\mathrm{for}\:\mathrm{x}\sim\mathrm{0}\:\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{sin}\left(\mathrm{3x}\right)\sim\mathrm{3x}\:\mathrm{and}\:\mathrm{sin}\left(\mathrm{2x}\right)\sim\mathrm{2x}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\sim\frac{\mathrm{ln}\left(\mathrm{3x}\right)}{\mathrm{ln}\left(\mathrm{2x}\right)}\:\:\mathrm{by}\:\mathrm{hospital}\:\mathrm{we}\:\mathrm{get}\:\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \mathrm{f}\left(\mathrm{x}\right)=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \frac{\frac{\mathrm{3}}{\mathrm{3x}}}{\frac{\mathrm{2}}{\mathrm{2x}}}\:=\mathrm{1} \\ $$
