
Question Number 126298 by bramlexs22 last updated on 19/Dec/20
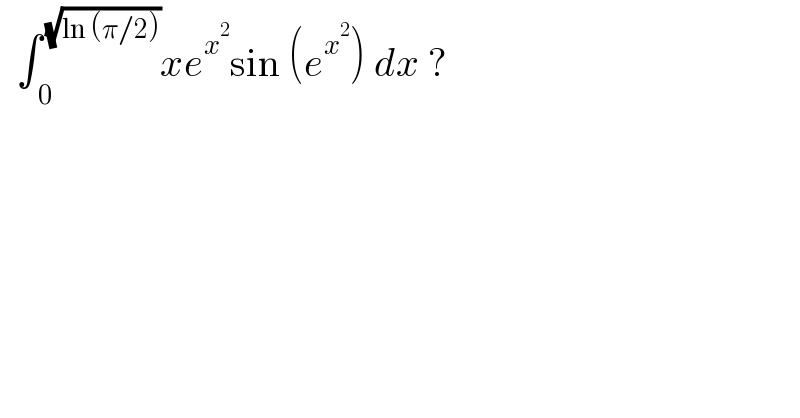
$$\:\:\int_{\:\mathrm{0}} ^{\:\sqrt{\mathrm{ln}\:\left(\pi/\mathrm{2}\right)}} {xe}^{{x}^{\mathrm{2}} } \mathrm{sin}\:\left({e}^{{x}^{\mathrm{2}} } \right)\:{dx}\:? \\ $$
Answered by liberty last updated on 19/Dec/20
![let v=e^x^2 ∧ dv=2xe^x^2 dx→ { ((x=0→v=1)),((x=(√(ln ((π/2))))→v=(π/2))) :} V=∫_1 ^( π/2) (1/2)sin v dv =−(1/2)[ cos v ]_1 ^(π/2) V=−(1/2)(0−cos 1)=(1/2)cos 1](Q126303.png)
$${let}\:{v}={e}^{{x}^{\mathrm{2}} } \wedge\:{dv}=\mathrm{2}{xe}^{{x}^{\mathrm{2}} } {dx}\rightarrow\begin{cases}{{x}=\mathrm{0}\rightarrow{v}=\mathrm{1}}\\{{x}=\sqrt{\mathrm{ln}\:\left(\frac{\pi}{\mathrm{2}}\right)}\rightarrow{v}=\frac{\pi}{\mathrm{2}}}\end{cases} \\ $$$${V}=\int_{\mathrm{1}} ^{\:\pi/\mathrm{2}} \frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:{v}\:{dv}\:=−\frac{\mathrm{1}}{\mathrm{2}}\left[\:\mathrm{cos}\:{v}\:\right]_{\mathrm{1}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$${V}=−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{0}−\mathrm{cos}\:\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{1} \\ $$
Answered by Olaf last updated on 19/Dec/20
![I = ∫_0 ^(√(ln(π/2))) xe^x^2 sin(e^x^2 )dx I = ∫_0 ^(√(ln(π/2))) −(1/2).(d/dx)cos(e^x^2 )dx I = −(1/2)[cos(e^x^2 )]_0 ^(√(ln(π/2))) = ((cos(1))/2)](Q126306.png)
$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{ln}\frac{\pi}{\mathrm{2}}}} {xe}^{{x}^{\mathrm{2}} } \mathrm{sin}\left({e}^{{x}^{\mathrm{2}} } \right){dx} \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{ln}\frac{\pi}{\mathrm{2}}}} −\frac{\mathrm{1}}{\mathrm{2}}.\frac{{d}}{{dx}}\mathrm{cos}\left({e}^{{x}^{\mathrm{2}} } \right){dx} \\ $$$$\mathrm{I}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{cos}\left({e}^{{x}^{\mathrm{2}} } \right)\right]_{\mathrm{0}} ^{\sqrt{\mathrm{ln}\frac{\pi}{\mathrm{2}}}} =\:\frac{\mathrm{cos}\left(\mathrm{1}\right)}{\mathrm{2}} \\ $$
Answered by Dwaipayan Shikari last updated on 19/Dec/20
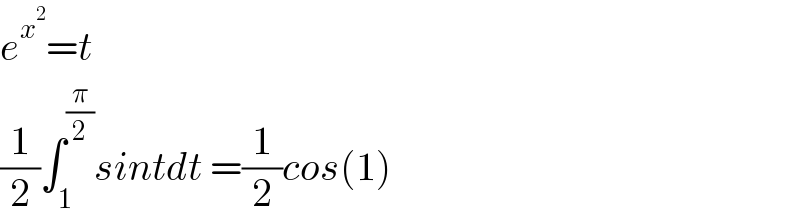
$${e}^{{x}^{\mathrm{2}} } ={t}\:\:\:\: \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\frac{\pi}{\mathrm{2}}} {sintdt}\:=\frac{\mathrm{1}}{\mathrm{2}}{cos}\left(\mathrm{1}\right) \\ $$
