
Previous in Differential Equation Next in Differential Equation
Question Number 126223 by liberty last updated on 18/Dec/20
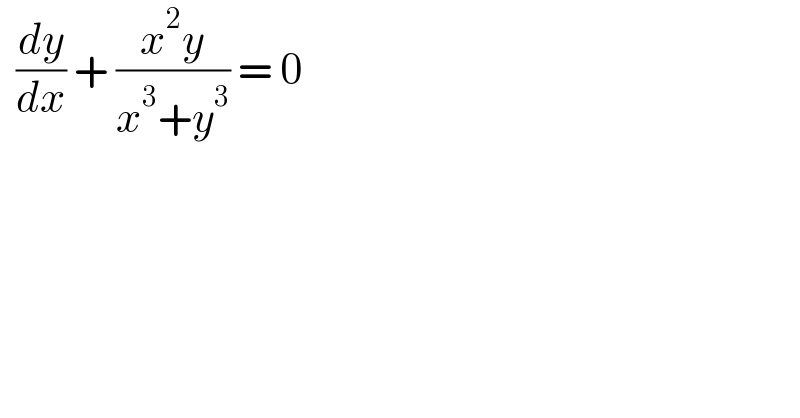
$$\:\:\frac{{dy}}{{dx}}\:+\:\frac{{x}^{\mathrm{2}} {y}}{{x}^{\mathrm{3}} +{y}^{\mathrm{3}} }\:=\:\mathrm{0} \\ $$
Commented by bramlexs22 last updated on 18/Dec/20
![v+x(dv/dx) = ((x^3 v)/(x^3 (1+v^3 ))) ; [ v =(y/x) ] v+x(dv/dx)=(v/(1+v^3 )) x(dv/dx) = ((−v^4 )/(1+v^3 )) ; (((1+v^3 )dv)/v^4 )+(dx/x) = 0 ∫ (v^(−4) +v^(−1) )dv+∫(dx/x) = C −(1/(3v^3 )) + ln (vx) = C −(x^3 /(3y^3 )) + ln (y) = C (x^3 /(3y^3 )) = ln (λy )⇒ ((3y^3 )/x^3 ) = (1/(ln (λy))) y^3 = (x^3 /(3ln (λy))) .](Q126224.png)
$$\:{v}+{x}\frac{{dv}}{{dx}}\:=\:\frac{{x}^{\mathrm{3}} {v}}{{x}^{\mathrm{3}} \left(\mathrm{1}+{v}^{\mathrm{3}} \right)}\:;\:\left[\:{v}\:=\frac{{y}}{{x}}\:\right]\: \\ $$$${v}+{x}\frac{{dv}}{{dx}}=\frac{{v}}{\mathrm{1}+{v}^{\mathrm{3}} } \\ $$$${x}\frac{{dv}}{{dx}}\:=\:\frac{−{v}^{\mathrm{4}} }{\mathrm{1}+{v}^{\mathrm{3}} }\:;\:\frac{\left(\mathrm{1}+{v}^{\mathrm{3}} \right){dv}}{{v}^{\mathrm{4}} }+\frac{{dx}}{{x}}\:=\:\mathrm{0} \\ $$$$\int\:\left({v}^{−\mathrm{4}} +{v}^{−\mathrm{1}} \right){dv}+\int\frac{{dx}}{{x}}\:=\:{C} \\ $$$$−\frac{\mathrm{1}}{\mathrm{3}{v}^{\mathrm{3}} }\:+\:\mathrm{ln}\:\left({vx}\right)\:=\:{C} \\ $$$$−\frac{{x}^{\mathrm{3}} }{\mathrm{3}{y}^{\mathrm{3}} }\:+\:\mathrm{ln}\:\left({y}\right)\:=\:{C}\: \\ $$$$\:\frac{{x}^{\mathrm{3}} }{\mathrm{3}{y}^{\mathrm{3}} }\:=\:\mathrm{ln}\:\left(\lambda{y}\:\right)\Rightarrow\:\frac{\mathrm{3}{y}^{\mathrm{3}} }{{x}^{\mathrm{3}} }\:=\:\frac{\mathrm{1}}{\mathrm{ln}\:\left(\lambda{y}\right)} \\ $$$${y}^{\mathrm{3}} \:=\:\frac{{x}^{\mathrm{3}} }{\mathrm{3ln}\:\left(\lambda{y}\right)}\:. \\ $$$$ \\ $$
