
Question Number 126030 by Fareed last updated on 16/Dec/20
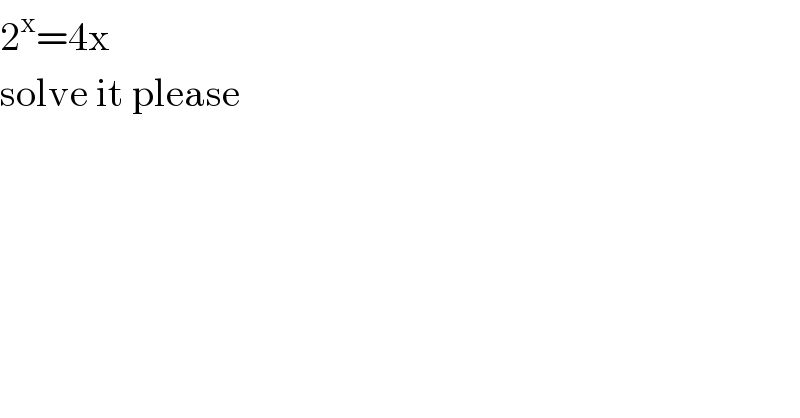
$$\mathrm{2}^{\mathrm{x}} =\mathrm{4x} \\ $$$$\mathrm{solve}\:\mathrm{it}\:\mathrm{please} \\ $$
Answered by Dwaipayan Shikari last updated on 16/Dec/20
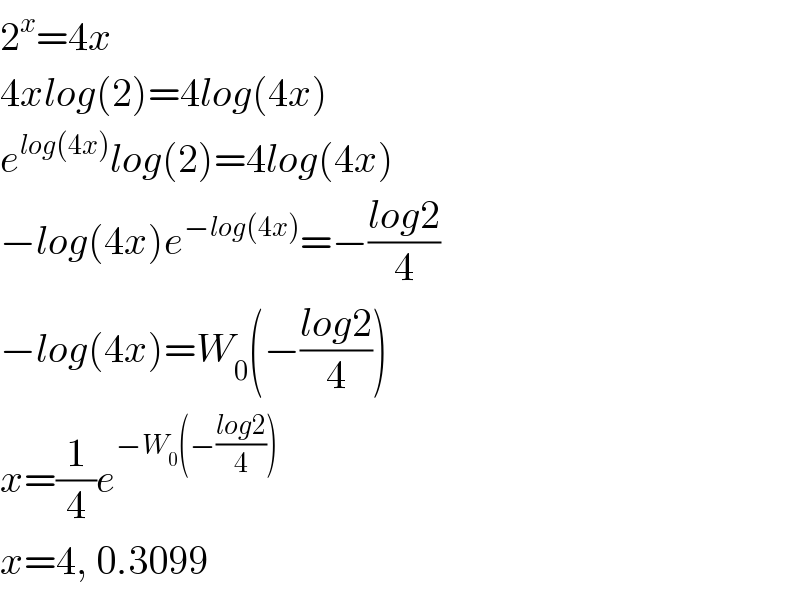
$$\mathrm{2}^{{x}} =\mathrm{4}{x} \\ $$$$\mathrm{4}{xlog}\left(\mathrm{2}\right)=\mathrm{4}{log}\left(\mathrm{4}{x}\right) \\ $$$${e}^{{log}\left(\mathrm{4}{x}\right)} {log}\left(\mathrm{2}\right)=\mathrm{4}{log}\left(\mathrm{4}{x}\right) \\ $$$$−{log}\left(\mathrm{4}{x}\right){e}^{−{log}\left(\mathrm{4}{x}\right)} =−\frac{{log}\mathrm{2}}{\mathrm{4}} \\ $$$$−{log}\left(\mathrm{4}{x}\right)={W}_{\mathrm{0}} \left(−\frac{{log}\mathrm{2}}{\mathrm{4}}\right) \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{4}}{e}^{−{W}_{\mathrm{0}} \left(−\frac{{log}\mathrm{2}}{\mathrm{4}}\right)} \:\:\:\: \\ $$$${x}=\mathrm{4},\:\mathrm{0}.\mathrm{3099} \\ $$
