
Question Number 125999 by bramlexs22 last updated on 16/Dec/20

Commented by bramlexs22 last updated on 16/Dec/20

$${thanks}\:{both}\:{sir} \\ $$
Answered by mr W last updated on 16/Dec/20
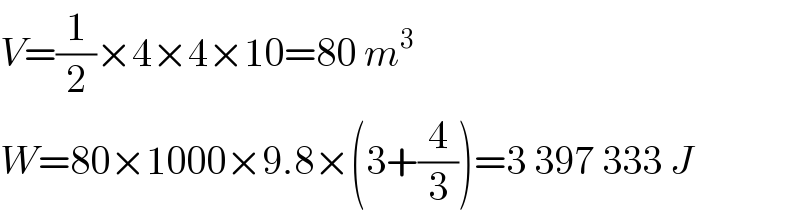
$${V}=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{4}×\mathrm{4}×\mathrm{10}=\mathrm{80}\:{m}^{\mathrm{3}} \\ $$$${W}=\mathrm{80}×\mathrm{1000}×\mathrm{9}.\mathrm{8}×\left(\mathrm{3}+\frac{\mathrm{4}}{\mathrm{3}}\right)=\mathrm{3}\:\mathrm{397}\:\mathrm{333}\:{J} \\ $$
Commented by bramlexs22 last updated on 16/Dec/20

$${by}\:{integral}\:{sir}? \\ $$
Commented by mr W last updated on 16/Dec/20

$${dW}=\rho{gzdV} \\ $$$${W}=\rho{g}\int{zdV}=\rho{gVz}_{{S}} \\ $$$${with}\:{z}_{{S}} ={distance}\:{to}\:{mass}\:{center} \\ $$$${this}\:{is}\:{valid}\:{for}\:{any}\:{shape}\:{of}\:{the} \\ $$$${water}\:{body}\:{to}\:{move}! \\ $$
Answered by liberty last updated on 16/Dec/20
![to find the weight of water , multiply the acceleration due to gravity , by the mass which equals to density of water multiplied by the volume : (9.8 m/s^2 )(1,000 kg/m^3 )(x_i ^∗ m)(Δx m)= 98,000(x_i ^∗ )(Δx) N ⇔ W= lim_(n→∞) Σ_(i=1) ^n (98,000)(x_i ^∗ )(7−x_i ^∗ )Δx ⇔ W = 98,000 ∫_0 ^( 4) x(7−x) dx = 98,000 [ (7/2)x^2 −(1/3)x^3 ]_0 ^4 = 98,000 ((7/2)4^2 −(1/3)4^3 )=((10,192,000)/3) J = 3,397,333 J](Q126019.png)
$${to}\:{find}\:{the}\:{weight}\:{of}\:{water}\:,\:{multiply}\: \\ $$$${the}\:{acceleration}\:{due}\:{to}\:{gravity}\:,\:{by}\:{the}\: \\ $$$${mass}\:{which}\:{equals}\:{to}\:{density}\:{of}\:{water} \\ $$$${multiplied}\:{by}\:{the}\:{volume}\::\: \\ $$$$\:\:\left(\mathrm{9}.\mathrm{8}\:{m}/{s}^{\mathrm{2}} \right)\left(\mathrm{1},\mathrm{000}\:{kg}/{m}^{\mathrm{3}} \right)\left({x}_{{i}} ^{\ast} \:{m}\right)\left(\Delta{x}\:{m}\right)= \\ $$$$\:\:\mathrm{98},\mathrm{000}\left({x}_{{i}} ^{\ast} \right)\left(\Delta{x}\right)\:{N} \\ $$$$\:\:\Leftrightarrow\:{W}=\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\mathrm{98},\mathrm{000}\right)\left({x}_{{i}} ^{\ast} \right)\left(\mathrm{7}−{x}_{{i}} ^{\ast} \right)\Delta{x} \\ $$$$\Leftrightarrow\:{W}\:=\:\mathrm{98},\mathrm{000}\:\int_{\mathrm{0}} ^{\:\mathrm{4}} {x}\left(\mathrm{7}−{x}\right)\:{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{98},\mathrm{000}\:\left[\:\frac{\mathrm{7}}{\mathrm{2}}{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{3}} \:\right]_{\mathrm{0}} ^{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{98},\mathrm{000}\:\left(\frac{\mathrm{7}}{\mathrm{2}}\mathrm{4}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}}\mathrm{4}^{\mathrm{3}} \right)=\frac{\mathrm{10},\mathrm{192},\mathrm{000}}{\mathrm{3}}\:{J} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{3},\mathrm{397},\mathrm{333}\:{J}\: \\ $$$$ \\ $$
