
Question Number 125965 by bramlexs22 last updated on 16/Dec/20
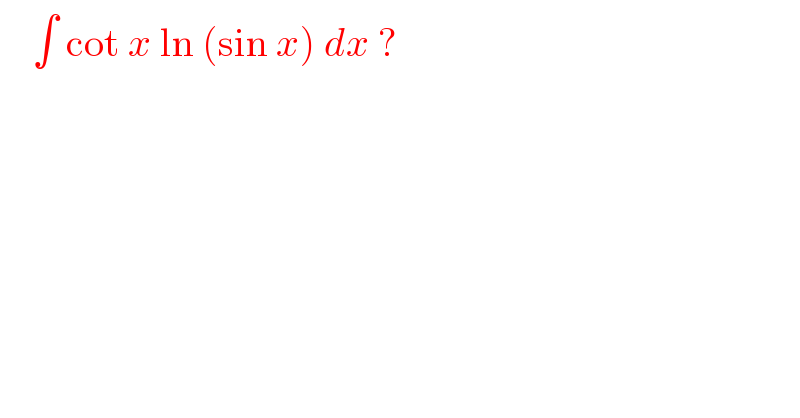
$$\:\:\:\:\int\:\mathrm{cot}\:{x}\:\mathrm{ln}\:\left(\mathrm{sin}\:{x}\right)\:{dx}\:? \\ $$
Answered by Lordose last updated on 16/Dec/20
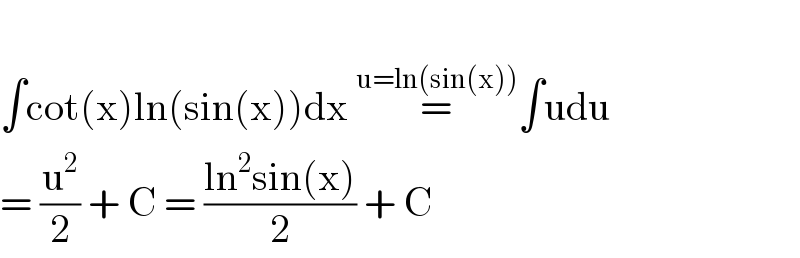
$$ \\ $$$$\int\mathrm{cot}\left(\mathrm{x}\right)\mathrm{ln}\left(\mathrm{sin}\left(\mathrm{x}\right)\right)\mathrm{dx}\:\overset{\mathrm{u}=\mathrm{ln}\left(\mathrm{sin}\left(\mathrm{x}\right)\right)} {=}\int\mathrm{udu}\:\:\: \\ $$$$=\:\frac{\mathrm{u}^{\mathrm{2}} }{\mathrm{2}}\:+\:\mathrm{C}\:=\:\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{sin}\left(\mathrm{x}\right)}{\mathrm{2}}\:+\:\mathrm{C} \\ $$
