
Question Number 125845 by joki last updated on 14/Dec/20
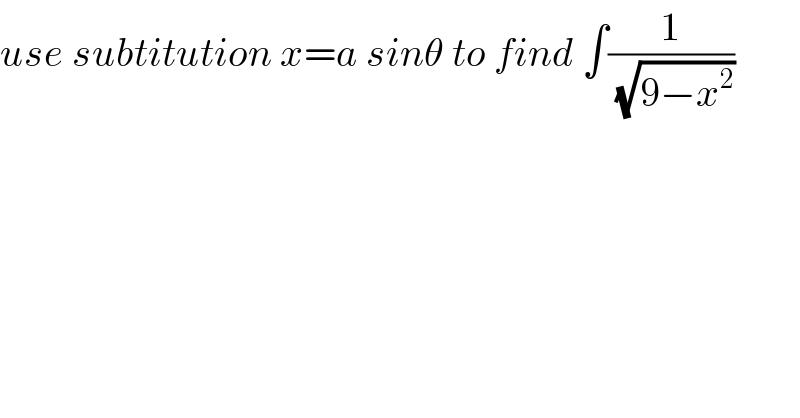
$${use}\:{subtitution}\:{x}={a}\:{sin}\theta\:{to}\:{find}\:\int\frac{\mathrm{1}}{\:\sqrt{\mathrm{9}−{x}^{\mathrm{2}} }} \\ $$
Answered by MJS_new last updated on 14/Dec/20
![∫(dx/( (√(9−x^2 ))))= [x=3sin θ ⇔ θ=arcsin (x/3) → dx=(√(9−x^2 ))dθ] =∫dθ=θ=arcsin (x/3) +C](Q125856.png)
$$\int\frac{{dx}}{\:\sqrt{\mathrm{9}−{x}^{\mathrm{2}} }}= \\ $$$$\:\:\:\:\:\left[{x}=\mathrm{3sin}\:\theta\:\Leftrightarrow\:\theta=\mathrm{arcsin}\:\frac{{x}}{\mathrm{3}}\:\rightarrow\:{dx}=\sqrt{\mathrm{9}−{x}^{\mathrm{2}} }{d}\theta\right] \\ $$$$=\int{d}\theta=\theta=\mathrm{arcsin}\:\frac{{x}}{\mathrm{3}}\:+{C} \\ $$
