
Question Number 125837 by joki last updated on 14/Dec/20

$${prove}\:{that}\:: \\ $$$$\int\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }{dx}=_{} \frac{{x}}{\mathrm{2}}\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }+\frac{{a}^{\mathrm{2}} }{\mathrm{2}}{sin}^{−\mathrm{1}} \left(\frac{{x}}{{a}}\right)+{c} \\ $$
Answered by Dwaipayan Shikari last updated on 14/Dec/20
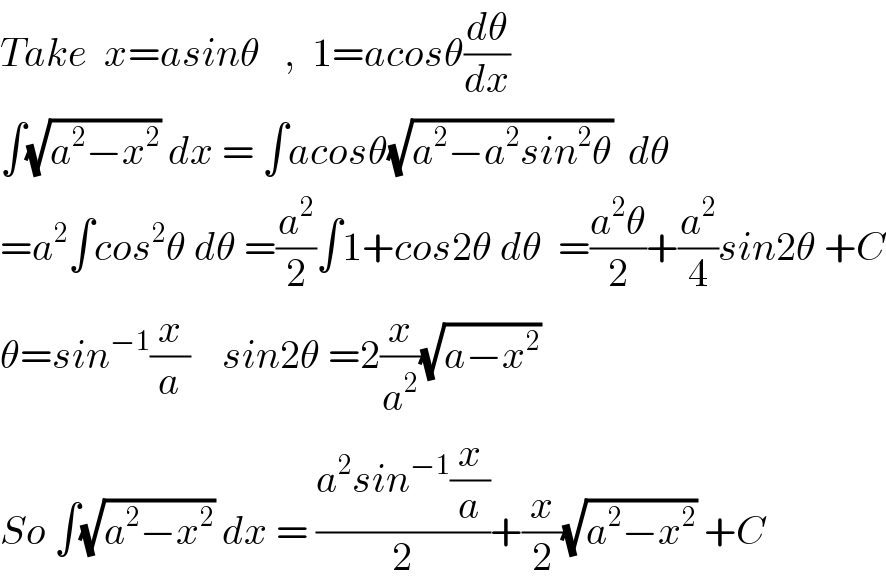
$${Take}\:\:{x}={asin}\theta\:\:\:,\:\:\mathrm{1}={acos}\theta\frac{{d}\theta}{{dx}} \\ $$$$\int\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }\:{dx}\:=\:\int{acos}\theta\sqrt{{a}^{\mathrm{2}} −{a}^{\mathrm{2}} {sin}^{\mathrm{2}} \theta}\:\:{d}\theta \\ $$$$={a}^{\mathrm{2}} \int{cos}^{\mathrm{2}} \theta\:{d}\theta\:=\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\int\mathrm{1}+{cos}\mathrm{2}\theta\:{d}\theta\:\:=\frac{{a}^{\mathrm{2}} \theta}{\mathrm{2}}+\frac{{a}^{\mathrm{2}} }{\mathrm{4}}{sin}\mathrm{2}\theta\:+{C} \\ $$$$\theta={sin}^{−\mathrm{1}} \frac{{x}}{{a}}\:\:\:\:{sin}\mathrm{2}\theta\:=\mathrm{2}\frac{{x}}{{a}^{\mathrm{2}} }\sqrt{{a}−{x}^{\mathrm{2}} } \\ $$$${So}\:\int\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }\:{dx}\:=\:\frac{{a}^{\mathrm{2}} {sin}^{−\mathrm{1}} \frac{{x}}{{a}}}{\mathrm{2}}+\frac{{x}}{\mathrm{2}}\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }\:+{C} \\ $$
