
Question Number 125686 by mathocean1 last updated on 12/Dec/20
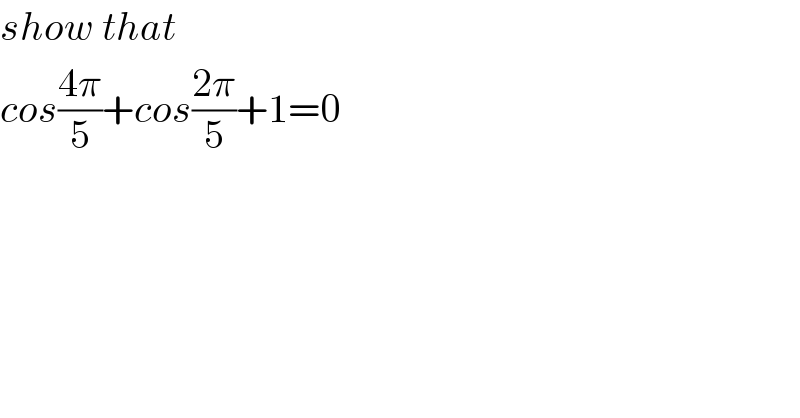
$${show}\:{that} \\ $$$${cos}\frac{\mathrm{4}\pi}{\mathrm{5}}+{cos}\frac{\mathrm{2}\pi}{\mathrm{5}}+\mathrm{1}=\mathrm{0} \\ $$
Commented by bramlexs22 last updated on 13/Dec/20
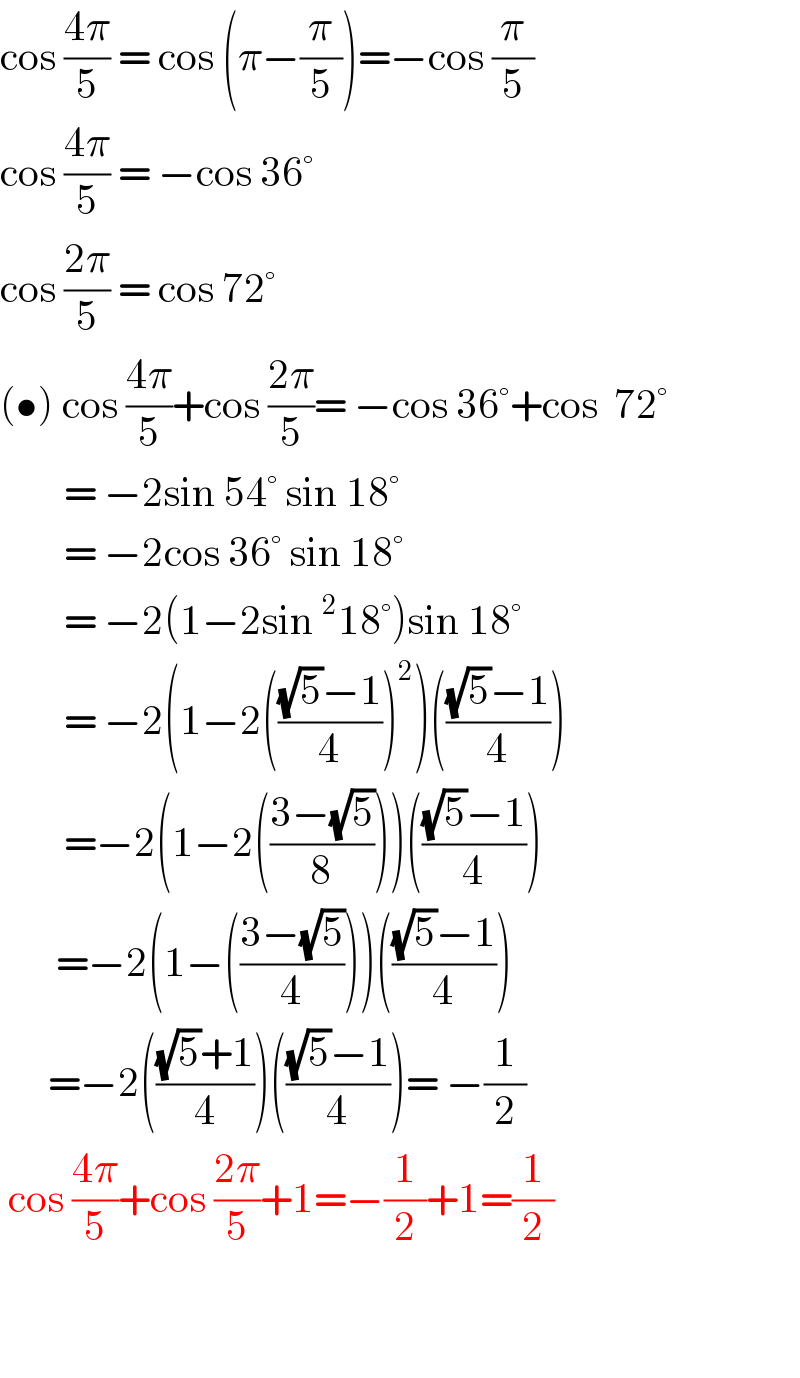
$$\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{5}}\:=\:\mathrm{cos}\:\left(\pi−\frac{\pi}{\mathrm{5}}\right)=−\mathrm{cos}\:\frac{\pi}{\mathrm{5}} \\ $$$$\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{5}}\:=\:−\mathrm{cos}\:\mathrm{36}°\: \\ $$$$\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{5}}\:=\:\mathrm{cos}\:\mathrm{72}° \\ $$$$\left(\bullet\right)\:\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{5}}+\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{5}}=\:−\mathrm{cos}\:\mathrm{36}°+\mathrm{cos}\:\:\mathrm{72}° \\ $$$$\:\:\:\:\:\:\:\:=\:−\mathrm{2sin}\:\mathrm{54}°\:\mathrm{sin}\:\mathrm{18}°\: \\ $$$$\:\:\:\:\:\:\:\:=\:−\mathrm{2cos}\:\mathrm{36}°\:\mathrm{sin}\:\mathrm{18}° \\ $$$$\:\:\:\:\:\:\:\:=\:−\mathrm{2}\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \mathrm{18}°\right)\mathrm{sin}\:\mathrm{18}° \\ $$$$\:\:\:\:\:\:\:\:=\:−\mathrm{2}\left(\mathrm{1}−\mathrm{2}\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} \right)\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}\right) \\ $$$$\:\:\:\:\:\:\:\:=−\mathrm{2}\left(\mathrm{1}−\mathrm{2}\left(\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{8}}\right)\right)\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}\right) \\ $$$$\:\:\:\:\:\:\:=−\mathrm{2}\left(\mathrm{1}−\left(\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{4}}\right)\right)\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}\right) \\ $$$$\:\:\:\:\:\:=−\mathrm{2}\left(\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{4}}\right)\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}\right)=\:−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{5}}+\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{5}}+\mathrm{1}=−\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{1}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$$$\: \\ $$
