Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 125670 by mathocean1 last updated on 12/Dec/20

N<10200 , N has five digits. N≡22[23] and N≡5[17]. Determinate the integer N.

$${N}<\mathrm{10200}\:,\:{N}\:{has}\:{five}\:{digits}. \\ $$ $${N}\equiv\mathrm{22}\left[\mathrm{23}\right]\:{and}\:{N}\equiv\mathrm{5}\left[\mathrm{17}\right]. \\ $$ $${Determinate}\:{the}\:{integer}\:{N}. \\ $$

Answered by floor(10²Eta[1]) last updated on 12/Dec/20

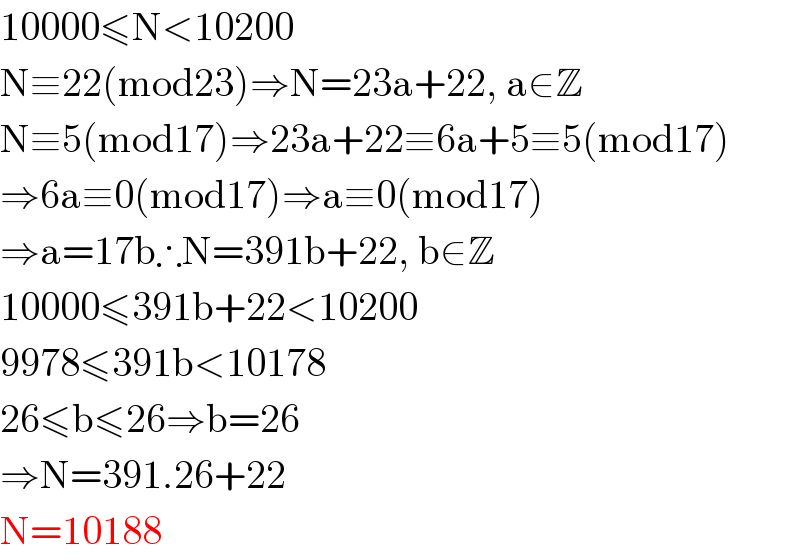
10000≤N<10200 N≡22(mod23)⇒N=23a+22, a∈Z N≡5(mod17)⇒23a+22≡6a+5≡5(mod17) ⇒6a≡0(mod17)⇒a≡0(mod17) ⇒a=17b∴N=391b+22, b∈Z 10000≤391b+22<10200 9978≤391b<10178 26≤b≤26⇒b=26 ⇒N=391.26+22 N=10188

$$\mathrm{10000}\leqslant\mathrm{N}<\mathrm{10200} \\ $$ $$\mathrm{N}\equiv\mathrm{22}\left(\mathrm{mod23}\right)\Rightarrow\mathrm{N}=\mathrm{23a}+\mathrm{22},\:\mathrm{a}\in\mathbb{Z} \\ $$ $$\mathrm{N}\equiv\mathrm{5}\left(\mathrm{mod17}\right)\Rightarrow\mathrm{23a}+\mathrm{22}\equiv\mathrm{6a}+\mathrm{5}\equiv\mathrm{5}\left(\mathrm{mod17}\right) \\ $$ $$\Rightarrow\mathrm{6a}\equiv\mathrm{0}\left(\mathrm{mod17}\right)\Rightarrow\mathrm{a}\equiv\mathrm{0}\left(\mathrm{mod17}\right) \\ $$ $$\Rightarrow\mathrm{a}=\mathrm{17b}\therefore\mathrm{N}=\mathrm{391b}+\mathrm{22},\:\mathrm{b}\in\mathbb{Z} \\ $$ $$\mathrm{10000}\leqslant\mathrm{391b}+\mathrm{22}<\mathrm{10200} \\ $$ $$\mathrm{9978}\leqslant\mathrm{391b}<\mathrm{10178} \\ $$ $$\mathrm{26}\leqslant\mathrm{b}\leqslant\mathrm{26}\Rightarrow\mathrm{b}=\mathrm{26} \\ $$ $$\Rightarrow\mathrm{N}=\mathrm{391}.\mathrm{26}+\mathrm{22} \\ $$ $$\mathrm{N}=\mathrm{10188} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com