
Question Number 125638 by aurpeyz last updated on 12/Dec/20

Answered by mathmax by abdo last updated on 12/Dec/20
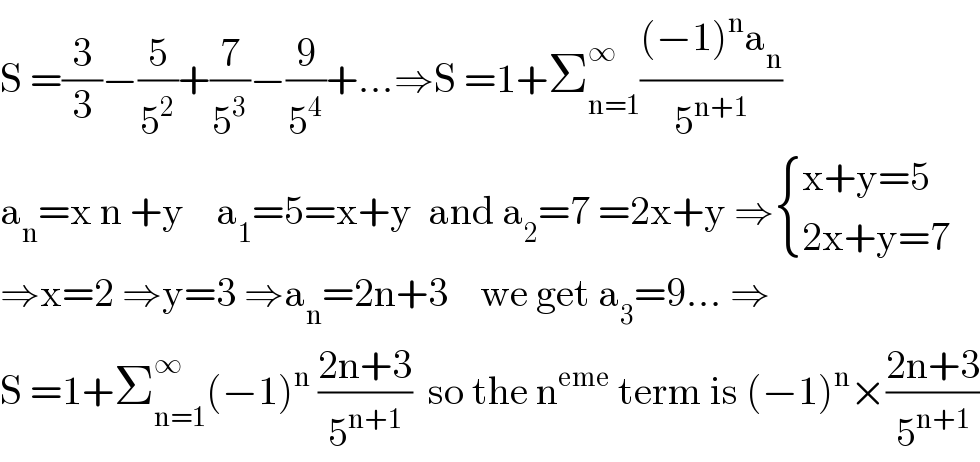
$$\mathrm{S}\:=\frac{\mathrm{3}}{\mathrm{3}}−\frac{\mathrm{5}}{\mathrm{5}^{\mathrm{2}} }+\frac{\mathrm{7}}{\mathrm{5}^{\mathrm{3}} }−\frac{\mathrm{9}}{\mathrm{5}^{\mathrm{4}} }+...\Rightarrow\mathrm{S}\:=\mathrm{1}+\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{a}_{\mathrm{n}} }{\mathrm{5}^{\mathrm{n}+\mathrm{1}} } \\ $$$$\mathrm{a}_{\mathrm{n}} =\mathrm{x}\:\mathrm{n}\:+\mathrm{y}\:\:\:\:\mathrm{a}_{\mathrm{1}} =\mathrm{5}=\mathrm{x}+\mathrm{y}\:\:\mathrm{and}\:\mathrm{a}_{\mathrm{2}} =\mathrm{7}\:=\mathrm{2x}+\mathrm{y}\:\Rightarrow\begin{cases}{\mathrm{x}+\mathrm{y}=\mathrm{5}}\\{\mathrm{2x}+\mathrm{y}=\mathrm{7}}\end{cases} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{2}\:\Rightarrow\mathrm{y}=\mathrm{3}\:\Rightarrow\mathrm{a}_{\mathrm{n}} =\mathrm{2n}+\mathrm{3}\:\:\:\:\mathrm{we}\:\mathrm{get}\:\mathrm{a}_{\mathrm{3}} =\mathrm{9}...\:\Rightarrow \\ $$$$\mathrm{S}\:=\mathrm{1}+\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \:\frac{\mathrm{2n}+\mathrm{3}}{\mathrm{5}^{\mathrm{n}+\mathrm{1}} }\:\:\mathrm{so}\:\mathrm{the}\:\mathrm{n}^{\mathrm{eme}} \:\mathrm{term}\:\mathrm{is}\:\left(−\mathrm{1}\right)^{\mathrm{n}} ×\frac{\mathrm{2n}+\mathrm{3}}{\mathrm{5}^{\mathrm{n}+\mathrm{1}} } \\ $$
Commented by aurpeyz last updated on 13/Dec/20

$${thanks} \\ $$
