
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 125548 by Don08q last updated on 12/Dec/20

$$\mathrm{How}\:\mathrm{many}\:\mathrm{four}−\mathrm{digit}\:\mathrm{numbers}\: \\ $$$$\mathrm{between}\:\mathrm{2000}\:\mathrm{and}\:\mathrm{4000}\:\mathrm{can}\:\mathrm{be}\:\mathrm{formed} \\ $$$$\mathrm{from}\:\mathrm{the}\:\mathrm{numbers}\:\mathrm{0},\:\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:\mathrm{4}\:\mathrm{and}\:\mathrm{5}\: \\ $$$$\mathrm{if}\:\mathrm{repitition}\:\mathrm{is}\:\mathrm{allowed}? \\ $$
Commented by liberty last updated on 13/Dec/20
![let the number ABCD where 2000<ABCD<4000 case(1) A_(2,3 [) B_(1,2,3,4,5]) CD = 2×5×6^2 = 360 case(2) A_(2,3) B_0 C_([1,2,3,4,5]) D = 2×1×5×6=60 case(3) A_(2,3) B_0 C_0 D_([ 1,2,3,4,5 ]) = 2×1×1×5=10 case(4) A_3 B_0 C_0 D_0 = 1×1×1×1=1 totally = 431](Q125555.png)
$${let}\:{the}\:{number}\:{ABCD}\:{where}\:\mathrm{2000}<{ABCD}<\mathrm{4000} \\ $$$${case}\left(\mathrm{1}\right)\:\underset{\mathrm{2},\mathrm{3}\:\:\left[\right.} {{A}}\underset{\left.\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{5}\right]} {{B}CD}\:=\:\mathrm{2}×\mathrm{5}×\mathrm{6}^{\mathrm{2}} \:=\:\mathrm{360} \\ $$$${case}\left(\mathrm{2}\right)\:\underset{\mathrm{2},\mathrm{3}} {{A}}\:\underset{\mathrm{0}} {{B}}\:\underset{\left[\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{5}\right]} {{C}}\:{D}\:=\:\mathrm{2}×\mathrm{1}×\mathrm{5}×\mathrm{6}=\mathrm{60} \\ $$$${case}\left(\mathrm{3}\right)\:\underset{\mathrm{2},\mathrm{3}} {{A}}\:\underset{\mathrm{0}} {{B}}\:\underset{\mathrm{0}} {{C}}\:\underset{\left[\:\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{5}\:\right]} {{D}}=\:\mathrm{2}×\mathrm{1}×\mathrm{1}×\mathrm{5}=\mathrm{10} \\ $$$${case}\left(\mathrm{4}\right)\:\underset{\mathrm{3}} {{A}}\:\underset{\mathrm{0}} {{B}}\:\underset{\mathrm{0}} {{C}}\:\underset{\mathrm{0}} {{D}}\:=\:\mathrm{1}×\mathrm{1}×\mathrm{1}×\mathrm{1}=\mathrm{1} \\ $$$${totally}\:=\:\mathrm{431}\: \\ $$
Commented by bemath last updated on 12/Dec/20
$${i}\:{think}\:{your}\:{answer}\:{correct}\:{sir} \\ $$
Answered by Olaf last updated on 12/Dec/20

$$\mathrm{The}\:\mathrm{first}\:\mathrm{digit}\:\mathrm{is}\:\mathrm{2}\:\mathrm{or}\:\mathrm{3}\:\Rightarrow\:\mathrm{2}\:\mathrm{possibilities}. \\ $$$$\mathrm{For}\:\mathrm{the}\:\mathrm{3}\:\mathrm{other}\:\mathrm{digits}\:\Rightarrow\:\mathrm{6}\:\mathrm{possibilities}. \\ $$$$\mathrm{2}×\mathrm{6}^{\mathrm{3}} \:=\:\mathrm{432} \\ $$$$\mathrm{Here}\:\mathrm{we}\:\mathrm{obtain}\:\mathrm{the}\:\mathrm{possibilities} \\ $$$$\mathrm{between}\:\mathrm{2000}\:\mathrm{and}\:\mathrm{3555}. \\ $$$$\mathrm{But}\:\mathrm{4000}\:\mathrm{is}\:\mathrm{a}\:\mathrm{possibility}\:\mathrm{too}. \\ $$$$\Rightarrow\:\mathrm{432}+\mathrm{1}\:=\:\mathrm{433}\:\mathrm{possibilities}. \\ $$
Commented by malwaan last updated on 12/Dec/20

$${mr}\:{olaf} \\ $$$${I}\:{think}\:{the}\:{right}\:{answer}\:{is}\: \\ $$$$\mathrm{432}−\mathrm{2}=\:\mathrm{430} \\ $$$${the}\:{question}\:{is}\:{between}\:\mathrm{2000} \\ $$$${and}\:\mathrm{4000} \\ $$$${If}\:\:{the}\:{question}\:\:{was}\:{from}\:\mathrm{2000}\: \\ $$$${to}\:\mathrm{4000}\:{then}\:{the}\:{answer}\:{will} \\ $$$${be}\:\mathrm{432} \\ $$
Commented by malwaan last updated on 12/Dec/20

$${sorry}\: \\ $$$${Iam}\:{not}\:{sure} \\ $$
Commented by mr W last updated on 12/Dec/20
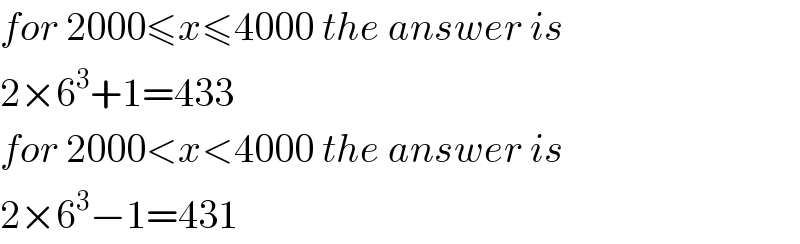
$${for}\:\mathrm{2000}\leqslant{x}\leqslant\mathrm{4000}\:{the}\:{answer}\:{is} \\ $$$$\mathrm{2}×\mathrm{6}^{\mathrm{3}} +\mathrm{1}=\mathrm{433} \\ $$$${for}\:\mathrm{2000}<{x}<\mathrm{4000}\:{the}\:{answer}\:{is} \\ $$$$\mathrm{2}×\mathrm{6}^{\mathrm{3}} −\mathrm{1}=\mathrm{431} \\ $$
Commented by Don08q last updated on 12/Dec/20
$$\mathrm{Yes}.\:\mathrm{431}\:\mathrm{is}\:\mathrm{the}\:\boldsymbol{\mathrm{correct}}\:\mathrm{answer}.\:\checkmark\checkmark \\ $$
Commented by Olaf last updated on 13/Dec/20

$$\mathrm{Sorry},\:\mathrm{my}\:\mathrm{english}\:\mathrm{is}\:\mathrm{not}\:\mathrm{fluent}. \\ $$$$\mathrm{In}\:\mathrm{my}\:\mathrm{language},\:``\mathrm{between}''\:\mathrm{means}\:\leqslant \\ $$
