
Question Number 125458 by mnjuly1970 last updated on 11/Dec/20
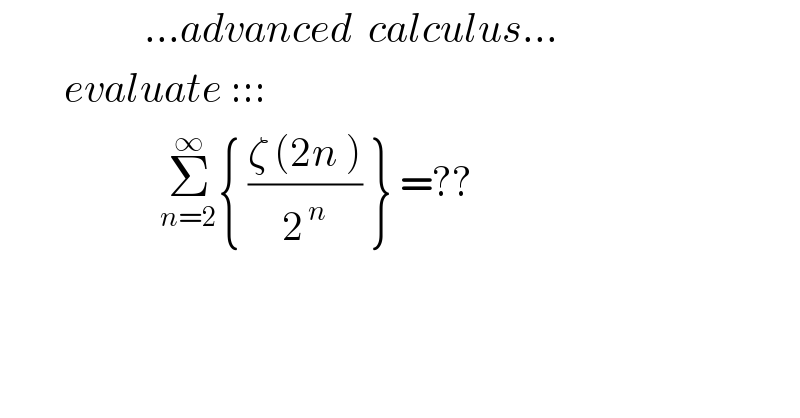
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:...{advanced}\:\:{calculus}... \\ $$$$\:\:\:\:\:\:\:\:{evaluate}\:::: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\left\{\:\frac{\zeta\:\left(\mathrm{2}{n}\:\right)}{\mathrm{2}^{\:{n}} }\:\right\}\:=?? \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 11/Dec/20
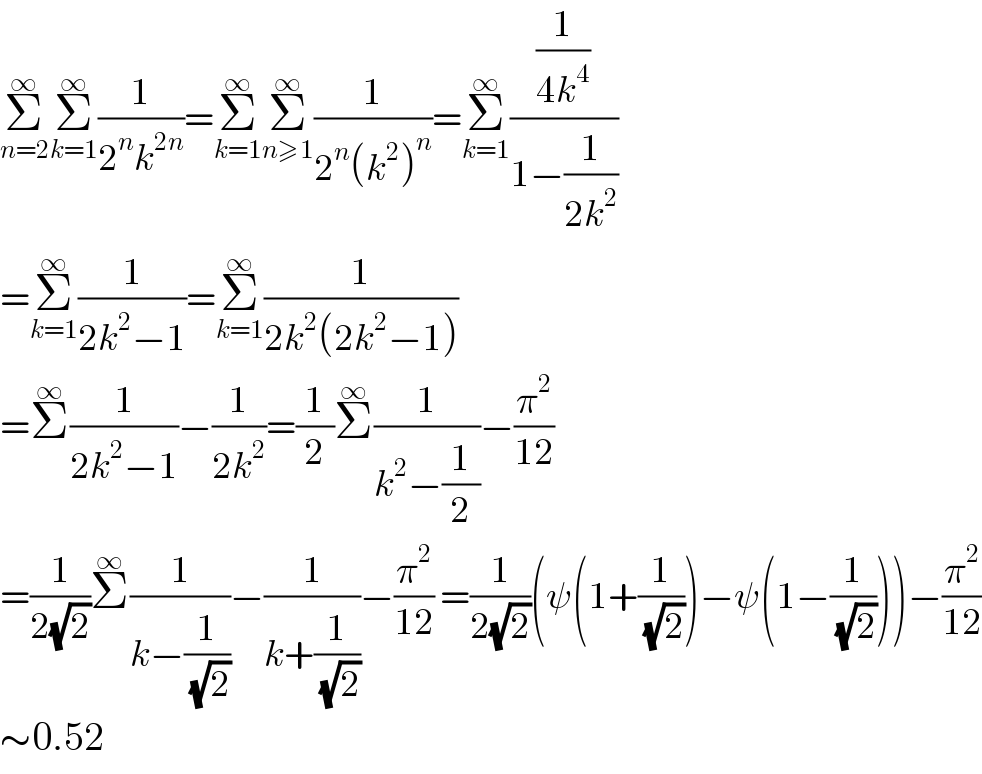
$$\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{n}} {k}^{\mathrm{2}{n}} }=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\underset{{n}\geqslant\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{n}} \left({k}^{\mathrm{2}} \right)^{{n}} }=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\frac{\mathrm{1}}{\mathrm{4}{k}^{\mathrm{4}} }}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{k}^{\mathrm{2}} }} \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}{k}^{\mathrm{2}} −\mathrm{1}}=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}{k}^{\mathrm{2}} \left(\mathrm{2}{k}^{\mathrm{2}} −\mathrm{1}\right)} \\ $$$$=\overset{\infty} {\sum}\frac{\mathrm{1}}{\mathrm{2}{k}^{\mathrm{2}} −\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}{k}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}}\overset{\infty} {\sum}\frac{\mathrm{1}}{{k}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}}−\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\overset{\infty} {\sum}\frac{\mathrm{1}}{{k}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}−\frac{\mathrm{1}}{{k}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left(\psi\left(\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)−\psi\left(\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)\right)−\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$$$\sim\mathrm{0}.\mathrm{52} \\ $$
Commented by Dwaipayan Shikari last updated on 11/Dec/20
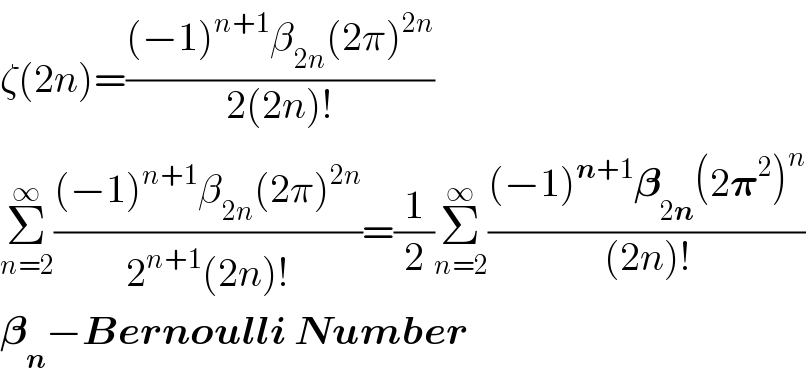
$$\zeta\left(\mathrm{2}{n}\right)=\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \beta_{\mathrm{2}{n}} \left(\mathrm{2}\pi\right)^{\mathrm{2}{n}} }{\mathrm{2}\left(\mathrm{2}{n}\right)!} \\ $$$$\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \beta_{\mathrm{2}{n}} \left(\mathrm{2}\pi\right)^{\mathrm{2}{n}} }{\mathrm{2}^{{n}+\mathrm{1}} \left(\mathrm{2}{n}\right)!}=\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\boldsymbol{{n}}+\mathrm{1}} \boldsymbol{\beta}_{\mathrm{2}\boldsymbol{{n}}} \left(\mathrm{2}\boldsymbol{\pi}^{\mathrm{2}} \right)^{{n}} }{\left(\mathrm{2}{n}\right)!} \\ $$$$\boldsymbol{\beta}_{\boldsymbol{{n}}} −\boldsymbol{{Bernoulli}}\:\boldsymbol{{Number}} \\ $$
Commented by mnjuly1970 last updated on 11/Dec/20
$${peace}\:{be}\:{upon}\:{you}... \\ $$
Commented by Dwaipayan Shikari last updated on 11/Dec/20
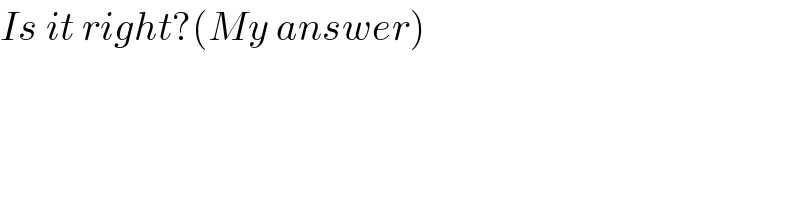
$${Is}\:{it}\:{right}?\left({My}\:{answer}\right) \\ $$
Commented by mnjuly1970 last updated on 11/Dec/20

$${yes}\:{of}\:{course}\:.\: \\ $$$$ \\ $$$$\:\:\:\:{but}\:{original}\:{question}\:{was}\:{as}\:{below}. \\ $$$$\:\:\:\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\zeta\left({n}\right)}{\mathrm{2}^{{n}} }\:\overset{??} {=}{log}\left(\mathrm{2}\right)... \\ $$
Commented by Dwaipayan Shikari last updated on 11/Dec/20
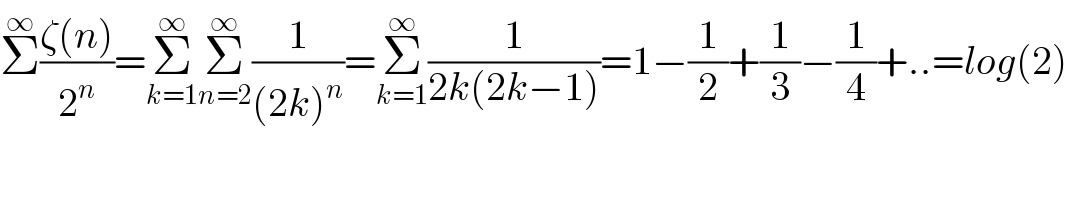
$$\overset{\infty} {\sum}\frac{\zeta\left({n}\right)}{\mathrm{2}^{{n}} }=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{k}\right)^{{n}} }=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}{k}\left(\mathrm{2}{k}−\mathrm{1}\right)}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{4}}+..={log}\left(\mathrm{2}\right) \\ $$
Commented by mnjuly1970 last updated on 11/Dec/20

$${perfect}.. \\ $$
Commented by Dwaipayan Shikari last updated on 11/Dec/20

$${With}\:{pleasure} \\ $$
Answered by mathmax by abdo last updated on 11/Dec/20

$$\sum_{\mathrm{n}=\mathrm{2}} ^{\infty} \frac{\xi\left(\mathrm{2n}\right)}{\mathrm{2}^{\mathrm{n}} }\:=\sum_{\mathrm{n}=\mathrm{2}} ^{\infty} \frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\sum_{\mathrm{k}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{2n}} }\:=\sum_{\mathrm{k}=\mathrm{1}} ^{\infty} \sum_{\mathrm{n}=\mathrm{2}} ^{\infty} \frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\frac{\mathrm{1}}{\left(\mathrm{k}^{\mathrm{2}} \right)^{\mathrm{n}} } \\ $$$$=\sum_{\mathrm{k}=\mathrm{1}} ^{\infty} \sum_{\mathrm{n}=\mathrm{2}} ^{\infty} \left(\frac{\mathrm{1}}{\mathrm{2k}^{\mathrm{2}} }\right)^{\mathrm{n}} \:\:=\sum_{\mathrm{k}=\mathrm{1}} ^{\infty} \sum_{\mathrm{p}=\mathrm{0}} ^{\infty} \left(\frac{\mathrm{1}}{\mathrm{2k}^{\mathrm{2}} }\right)^{\mathrm{p}+\mathrm{2}} \\ $$$$=\sum_{\mathrm{k}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{4k}^{\mathrm{4}} }\sum_{\mathrm{p}=\mathrm{0}} ^{\infty} \:\left(\frac{\mathrm{1}}{\mathrm{2k}^{\mathrm{2}} }\right)^{\mathrm{p}} \:=\sum_{\mathrm{k}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{4k}^{\mathrm{4}} }×\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2k}^{\mathrm{2}} }} \\ $$$$=\sum_{\mathrm{k}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{2k}^{\mathrm{2}} }{\mathrm{4k}^{\mathrm{4}} \left(\mathrm{2k}^{\mathrm{2}} −\mathrm{1}\right)}\:=\sum_{\mathrm{k}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{\mathrm{2k}^{\mathrm{2}} \left(\mathrm{2k}^{\mathrm{2}} −\mathrm{1}\right)} \\ $$$$=\sum_{\mathrm{k}=\mathrm{1}} ^{\infty} \left(\frac{\mathrm{1}}{\mathrm{2k}^{\mathrm{2}} −\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2k}^{\mathrm{2}} }\right)=\sum_{\mathrm{k}=\mathrm{1}} ^{\infty} \frac{\mathrm{1}}{\mathrm{2k}^{\mathrm{2}} −\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}×\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$=\sum_{\mathrm{k}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{2k}^{\mathrm{2}} −\mathrm{1}}−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\:\:\mathrm{rest}\:\mathrm{to}\:\mathrm{find}\:\mathrm{value}\:\mathrm{of}\:\sum_{\mathrm{k}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{2k}^{\mathrm{2}} −\mathrm{1}} \\ $$$$...\mathrm{be}\:\mathrm{continued}... \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 11/Dec/20
$${thanks}\:{alot}\:{sir}... \\ $$
Commented by mathmax by abdo last updated on 11/Dec/20

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome}\:\mathrm{sir}. \\ $$
