Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 125322 by john_santu last updated on 10/Dec/20

Commented by john_santu last updated on 10/Dec/20

question (c)

$${question}\:\left({c}\right) \\ $$

Commented by john_santu last updated on 10/Dec/20

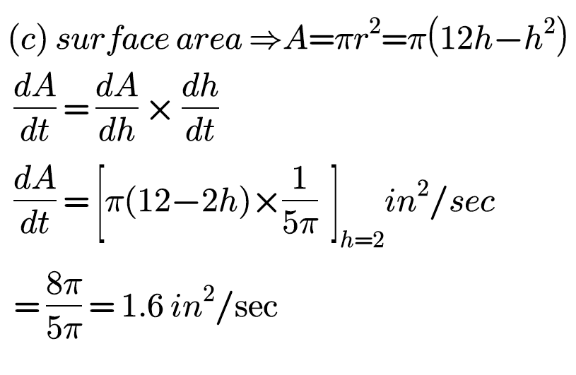
Commented by john_santu last updated on 10/Dec/20

is it correct ?

$${is}\:{it}\:{correct}\:? \\ $$

Commented by mr W last updated on 10/Dec/20

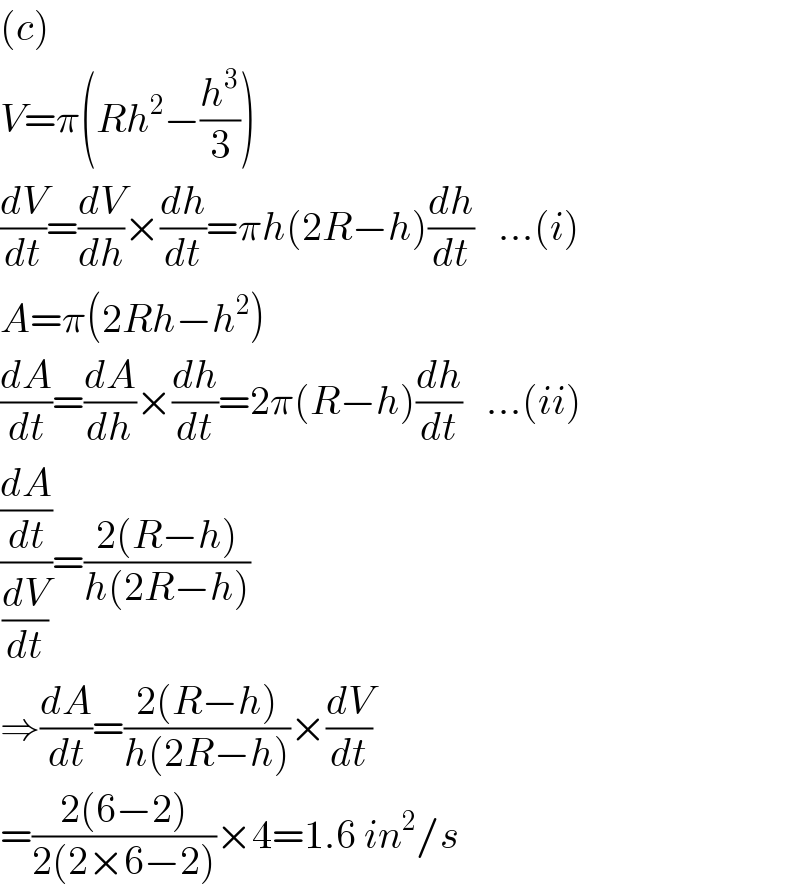
(c) V=π(Rh^2 −(h^3 /3)) (dV/dt)=(dV/dh)×(dh/dt)=πh(2R−h)(dh/dt) ...(i) A=π(2Rh−h^2 ) (dA/dt)=(dA/dh)×(dh/dt)=2π(R−h)(dh/dt) ...(ii) ((dA/dt)/(dV/dt))=((2(R−h))/(h(2R−h))) ⇒(dA/dt)=((2(R−h))/(h(2R−h)))×(dV/dt) =((2(6−2))/(2(2×6−2)))×4=1.6 in^2 /s

$$\left({c}\right) \\ $$$${V}=\pi\left({Rh}^{\mathrm{2}} −\frac{{h}^{\mathrm{3}} }{\mathrm{3}}\right) \\ $$$$\frac{{dV}}{{dt}}=\frac{{dV}}{{dh}}×\frac{{dh}}{{dt}}=\pi{h}\left(\mathrm{2}{R}−{h}\right)\frac{{dh}}{{dt}}\:\:\:...\left({i}\right) \\ $$$${A}=\pi\left(\mathrm{2}{Rh}−{h}^{\mathrm{2}} \right) \\ $$$$\frac{{dA}}{{dt}}=\frac{{dA}}{{dh}}×\frac{{dh}}{{dt}}=\mathrm{2}\pi\left({R}−{h}\right)\frac{{dh}}{{dt}}\:\:\:...\left({ii}\right) \\ $$$$\frac{\frac{{dA}}{{dt}}}{\frac{{dV}}{{dt}}}=\frac{\mathrm{2}\left({R}−{h}\right)}{{h}\left(\mathrm{2}{R}−{h}\right)} \\ $$$$\Rightarrow\frac{{dA}}{{dt}}=\frac{\mathrm{2}\left({R}−{h}\right)}{{h}\left(\mathrm{2}{R}−{h}\right)}×\frac{{dV}}{{dt}} \\ $$$$=\frac{\mathrm{2}\left(\mathrm{6}−\mathrm{2}\right)}{\mathrm{2}\left(\mathrm{2}×\mathrm{6}−\mathrm{2}\right)}×\mathrm{4}=\mathrm{1}.\mathrm{6}\:{in}^{\mathrm{2}} /{s} \\ $$

Commented by john_santu last updated on 10/Dec/20

ok correct . thanks

$${ok}\:{correct}\:.\:{thanks} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com