
Question Number 125266 by ZiYangLee last updated on 09/Dec/20
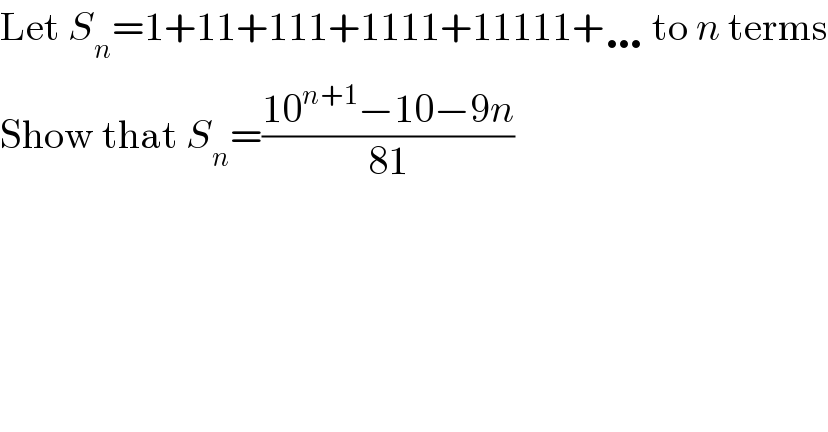
$$\mathrm{Let}\:{S}_{{n}} =\mathrm{1}+\mathrm{11}+\mathrm{111}+\mathrm{1111}+\mathrm{11111}+\ldots\:\mathrm{to}\:{n}\:\mathrm{terms} \\ $$$$\mathrm{Show}\:\mathrm{that}\:{S}_{{n}} =\frac{\mathrm{10}^{{n}+\mathrm{1}} −\mathrm{10}−\mathrm{9}{n}}{\mathrm{81}} \\ $$
Answered by Dwaipayan Shikari last updated on 09/Dec/20
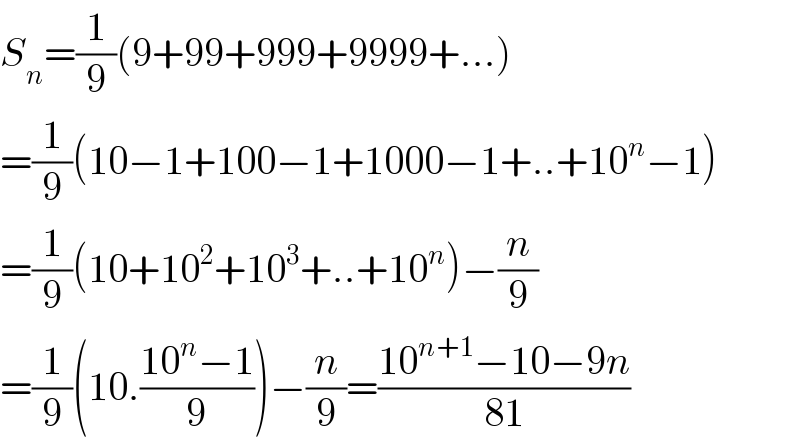
$${S}_{{n}} =\frac{\mathrm{1}}{\mathrm{9}}\left(\mathrm{9}+\mathrm{99}+\mathrm{999}+\mathrm{9999}+...\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}\left(\mathrm{10}−\mathrm{1}+\mathrm{100}−\mathrm{1}+\mathrm{1000}−\mathrm{1}+..+\mathrm{10}^{{n}} −\mathrm{1}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}\left(\mathrm{10}+\mathrm{10}^{\mathrm{2}} +\mathrm{10}^{\mathrm{3}} +..+\mathrm{10}^{{n}} \right)−\frac{{n}}{\mathrm{9}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}\left(\mathrm{10}.\frac{\mathrm{10}^{{n}} −\mathrm{1}}{\mathrm{9}}\right)−\frac{{n}}{\mathrm{9}}=\frac{\mathrm{10}^{{n}+\mathrm{1}} −\mathrm{10}−\mathrm{9}{n}}{\mathrm{81}} \\ $$
Commented by Dwaipayan Shikari last updated on 09/Dec/20
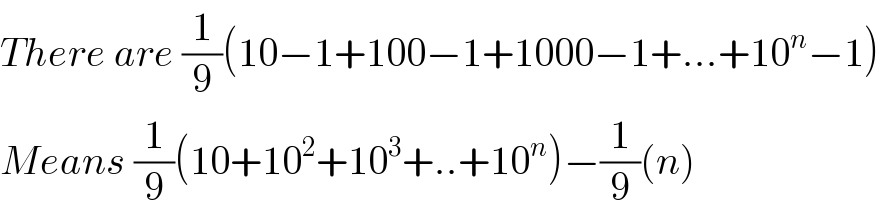
$${There}\:{are}\:\frac{\mathrm{1}}{\mathrm{9}}\left(\mathrm{10}−\mathrm{1}+\mathrm{100}−\mathrm{1}+\mathrm{1000}−\mathrm{1}+...+\mathrm{10}^{{n}} −\mathrm{1}\right) \\ $$$${Means}\:\frac{\mathrm{1}}{\mathrm{9}}\left(\mathrm{10}+\mathrm{10}^{\mathrm{2}} +\mathrm{10}^{\mathrm{3}} +..+\mathrm{10}^{{n}} \right)−\frac{\mathrm{1}}{\mathrm{9}}\left({n}\right) \\ $$
Commented by ZiYangLee last updated on 09/Dec/20
$$\mathrm{oh}\:\mathrm{I}\:\mathrm{see}!\:\mathrm{Thanks}\:\mathrm{very}\:\mathrm{much}! \\ $$
