
Question Number 12525 by tawa last updated on 24/Apr/17
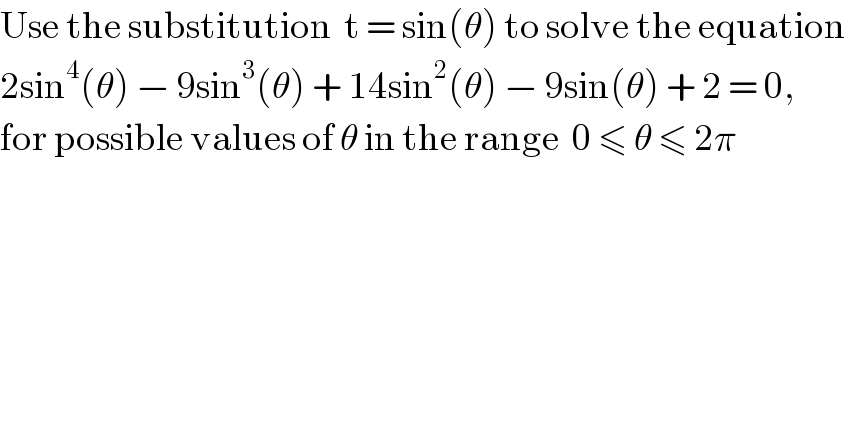
$$\mathrm{Use}\:\mathrm{the}\:\mathrm{substitution}\:\:\mathrm{t}\:=\:\mathrm{sin}\left(\theta\right)\:\mathrm{to}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{equation}\: \\ $$$$\mathrm{2sin}^{\mathrm{4}} \left(\theta\right)\:−\:\mathrm{9sin}^{\mathrm{3}} \left(\theta\right)\:+\:\mathrm{14sin}^{\mathrm{2}} \left(\theta\right)\:−\:\mathrm{9sin}\left(\theta\right)\:+\:\mathrm{2}\:=\:\mathrm{0},\:\: \\ $$$$\mathrm{for}\:\mathrm{possible}\:\mathrm{values}\:\mathrm{of}\:\theta\:\mathrm{in}\:\mathrm{the}\:\mathrm{range}\:\:\mathrm{0}\:\leqslant\:\theta\:\leqslant\:\mathrm{2}\pi \\ $$
Answered by mrW1 last updated on 24/Apr/17
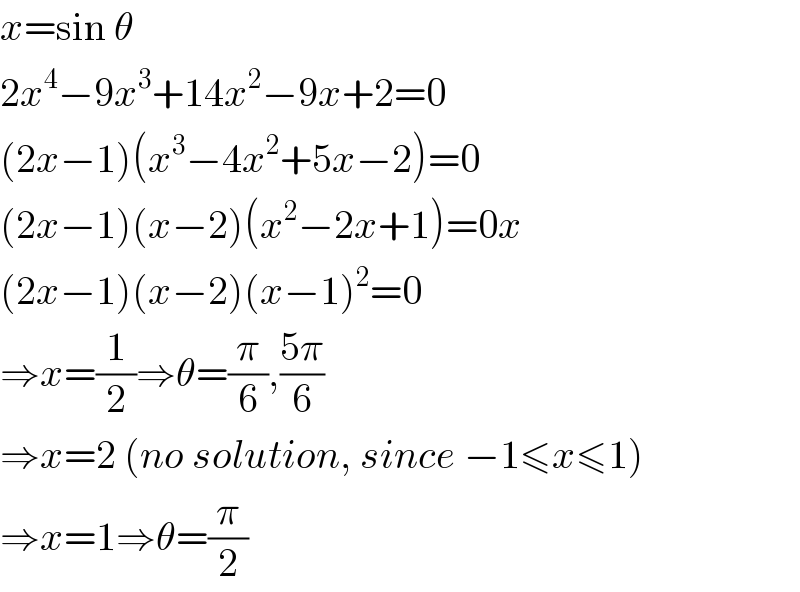
$${x}=\mathrm{sin}\:\theta \\ $$$$\mathrm{2}{x}^{\mathrm{4}} −\mathrm{9}{x}^{\mathrm{3}} +\mathrm{14}{x}^{\mathrm{2}} −\mathrm{9}{x}+\mathrm{2}=\mathrm{0} \\ $$$$\left(\mathrm{2}{x}−\mathrm{1}\right)\left({x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} +\mathrm{5}{x}−\mathrm{2}\right)=\mathrm{0} \\ $$$$\left(\mathrm{2}{x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)\left({x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}\right)=\mathrm{0}{x} \\ $$$$\left(\mathrm{2}{x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)\left({x}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\theta=\frac{\pi}{\mathrm{6}},\frac{\mathrm{5}\pi}{\mathrm{6}} \\ $$$$\Rightarrow{x}=\mathrm{2}\:\left({no}\:{solution},\:{since}\:−\mathrm{1}\leqslant{x}\leqslant\mathrm{1}\right) \\ $$$$\Rightarrow{x}=\mathrm{1}\Rightarrow\theta=\frac{\pi}{\mathrm{2}} \\ $$
Commented by tawa last updated on 24/Apr/17
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{Thanks}\:\mathrm{for}\:\mathrm{the}\:\mathrm{help}. \\ $$
Answered by sma3l2996 last updated on 24/Apr/17
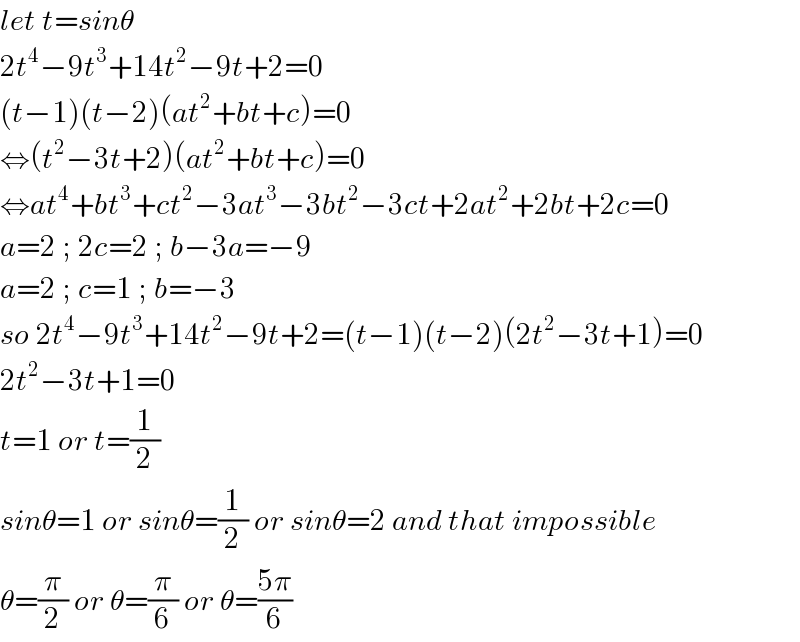
$${let}\:{t}={sin}\theta \\ $$$$\mathrm{2}{t}^{\mathrm{4}} −\mathrm{9}{t}^{\mathrm{3}} +\mathrm{14}{t}^{\mathrm{2}} −\mathrm{9}{t}+\mathrm{2}=\mathrm{0} \\ $$$$\left({t}−\mathrm{1}\right)\left({t}−\mathrm{2}\right)\left({at}^{\mathrm{2}} +{bt}+{c}\right)=\mathrm{0} \\ $$$$\Leftrightarrow\left({t}^{\mathrm{2}} −\mathrm{3}{t}+\mathrm{2}\right)\left({at}^{\mathrm{2}} +{bt}+{c}\right)=\mathrm{0} \\ $$$$\Leftrightarrow{at}^{\mathrm{4}} +{bt}^{\mathrm{3}} +{ct}^{\mathrm{2}} −\mathrm{3}{at}^{\mathrm{3}} −\mathrm{3}{bt}^{\mathrm{2}} −\mathrm{3}{ct}+\mathrm{2}{at}^{\mathrm{2}} +\mathrm{2}{bt}+\mathrm{2}{c}=\mathrm{0} \\ $$$${a}=\mathrm{2}\:;\:\mathrm{2}{c}=\mathrm{2}\:;\:{b}−\mathrm{3}{a}=−\mathrm{9} \\ $$$${a}=\mathrm{2}\:;\:{c}=\mathrm{1}\:;\:{b}=−\mathrm{3} \\ $$$${so}\:\mathrm{2}{t}^{\mathrm{4}} −\mathrm{9}{t}^{\mathrm{3}} +\mathrm{14}{t}^{\mathrm{2}} −\mathrm{9}{t}+\mathrm{2}=\left({t}−\mathrm{1}\right)\left({t}−\mathrm{2}\right)\left(\mathrm{2}{t}^{\mathrm{2}} −\mathrm{3}{t}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{2}{t}^{\mathrm{2}} −\mathrm{3}{t}+\mathrm{1}=\mathrm{0} \\ $$$${t}=\mathrm{1}\:{or}\:{t}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${sin}\theta=\mathrm{1}\:{or}\:{sin}\theta=\frac{\mathrm{1}}{\mathrm{2}}\:{or}\:{sin}\theta=\mathrm{2}\:{and}\:{that}\:{impossible} \\ $$$$\theta=\frac{\pi}{\mathrm{2}}\:{or}\:\theta=\frac{\pi}{\mathrm{6}}\:{or}\:\theta=\frac{\mathrm{5}\pi}{\mathrm{6}} \\ $$
Commented by tawa last updated on 24/Apr/17
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{Thanks}\:\mathrm{for}\:\mathrm{the}\:\mathrm{help}. \\ $$
