
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 125208 by liberty last updated on 09/Dec/20
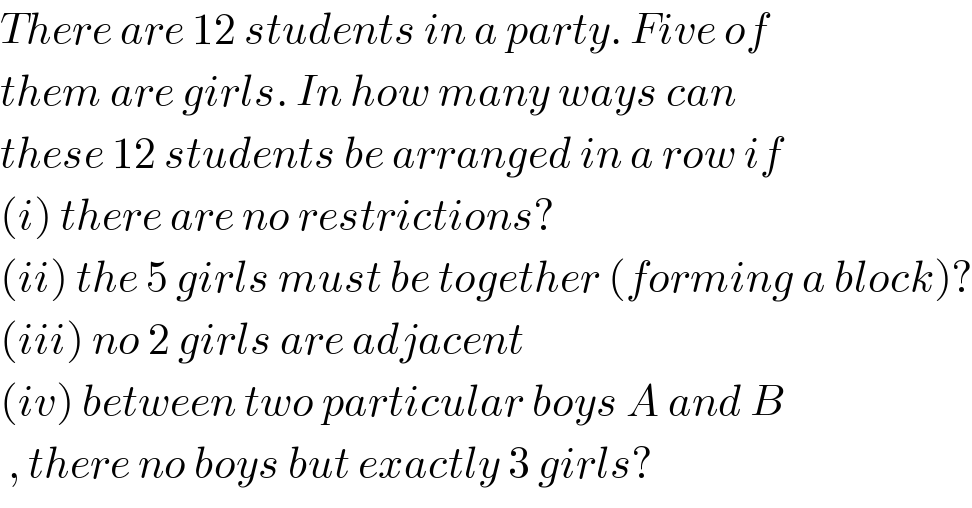
$${There}\:{are}\:\mathrm{12}\:{students}\:{in}\:{a}\:{party}.\:{Five}\:{of} \\ $$$${them}\:{are}\:{girls}.\:{In}\:{how}\:{many}\:{ways}\:{can}\: \\ $$$${these}\:\mathrm{12}\:{students}\:{be}\:{arranged}\:{in}\:{a}\:{row}\:{if}\: \\ $$$$\left({i}\right)\:{there}\:{are}\:{no}\:{restrictions}? \\ $$$$\left({ii}\right)\:{the}\:\mathrm{5}\:{girls}\:{must}\:{be}\:{together}\:\left({forming}\:{a}\:{block}\right)? \\ $$$$\left({iii}\right)\:{no}\:\mathrm{2}\:{girls}\:{are}\:{adjacent}\: \\ $$$$\left({iv}\right)\:{between}\:{two}\:{particular}\:{boys}\:{A}\:{and}\:{B}\: \\ $$$$\:,\:{there}\:{no}\:{boys}\:{but}\:{exactly}\:\mathrm{3}\:{girls}? \\ $$
Answered by john_santu last updated on 09/Dec/20
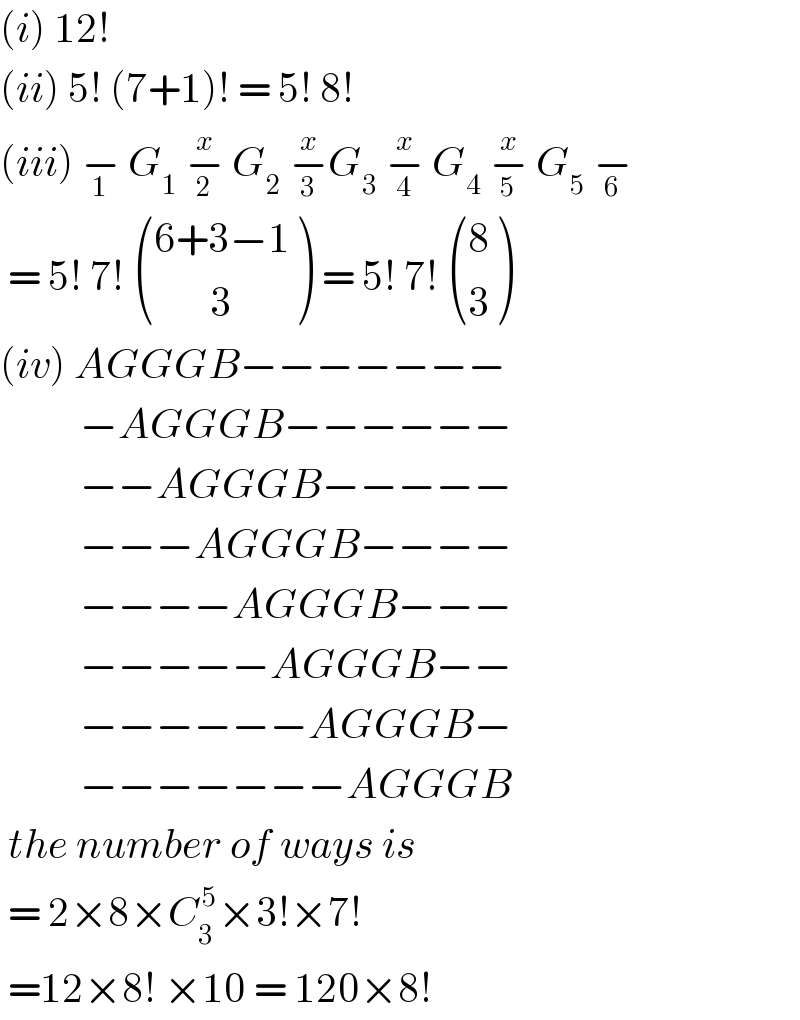
$$\left({i}\right)\:\mathrm{12}!\: \\ $$$$\left({ii}\right)\:\mathrm{5}!\:\left(\mathrm{7}+\mathrm{1}\right)!\:=\:\mathrm{5}!\:\mathrm{8}! \\ $$$$\left({iii}\right)\:\underset{\mathrm{1}} {−}\:{G}_{\mathrm{1}} \:\underset{\mathrm{2}} {\overset{{x}} {−}}\:{G}_{\mathrm{2}} \:\underset{\mathrm{3}} {\overset{{x}} {−}}{G}_{\mathrm{3}} \:\underset{\mathrm{4}} {\overset{{x}} {−}}\:{G}_{\mathrm{4}} \:\underset{\mathrm{5}} {\overset{{x}} {−}}\:{G}_{\mathrm{5}} \:\underset{\mathrm{6}} {−} \\ $$$$\:=\:\mathrm{5}!\:\mathrm{7}!\:\begin{pmatrix}{\mathrm{6}+\mathrm{3}−\mathrm{1}}\\{\:\:\:\:\:\:\:\mathrm{3}}\end{pmatrix}\:=\:\mathrm{5}!\:\mathrm{7}!\:\begin{pmatrix}{\mathrm{8}}\\{\mathrm{3}}\end{pmatrix} \\ $$$$\left({iv}\right)\:{AGGGB}−−−−−−− \\ $$$$\:\:\:\:\:\:\:\:\:\:−{AGGGB}−−−−−− \\ $$$$\:\:\:\:\:\:\:\:\:\:−−{AGGGB}−−−−− \\ $$$$\:\:\:\:\:\:\:\:\:\:−−−{AGGGB}−−−− \\ $$$$\:\:\:\:\:\:\:\:\:\:−−−−{AGGGB}−−− \\ $$$$\:\:\:\:\:\:\:\:\:\:−−−−−{AGGGB}−− \\ $$$$\:\:\:\:\:\:\:\:\:\:−−−−−−{AGGGB}− \\ $$$$\:\:\:\:\:\:\:\:\:\:−−−−−−−{AGGGB} \\ $$$$\:{the}\:{number}\:{of}\:{ways}\:{is}\: \\ $$$$\:=\:\mathrm{2}×\mathrm{8}×{C}_{\mathrm{3}} ^{\:\mathrm{5}} ×\mathrm{3}!×\mathrm{7}! \\ $$$$\:=\mathrm{12}×\mathrm{8}!\:×\mathrm{10}\:=\:\mathrm{120}×\mathrm{8}! \\ $$
Commented by liberty last updated on 09/Dec/20
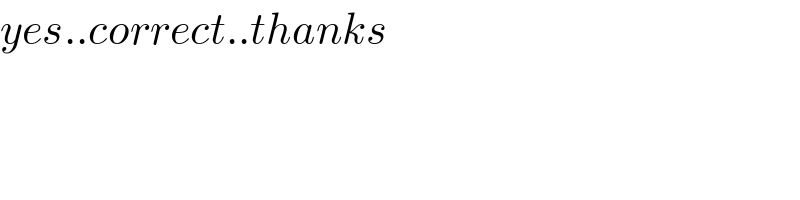
$${yes}..{correct}..{thanks} \\ $$
Commented by malwan last updated on 16/Jan/21
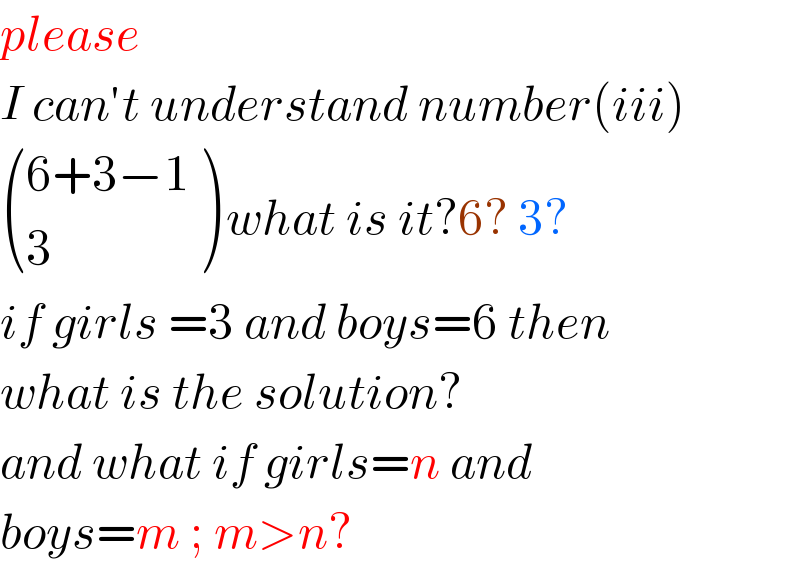
$${please} \\ $$$${I}\:{can}'{t}\:{understand}\:{number}\left({iii}\right) \\ $$$$\begin{pmatrix}{\mathrm{6}+\mathrm{3}−\mathrm{1}}\\{\mathrm{3}}\end{pmatrix}\:{what}\:{is}\:{it}?\mathrm{6}?\:\mathrm{3}? \\ $$$${if}\:{girls}\:=\mathrm{3}\:{and}\:{boys}=\mathrm{6}\:{then} \\ $$$${what}\:{is}\:{the}\:{solution}? \\ $$$${and}\:{what}\:{if}\:{girls}={n}\:{and} \\ $$$${boys}={m}\:;\:{m}>{n}? \\ $$
