
Question Number 125136 by Snail last updated on 08/Dec/20
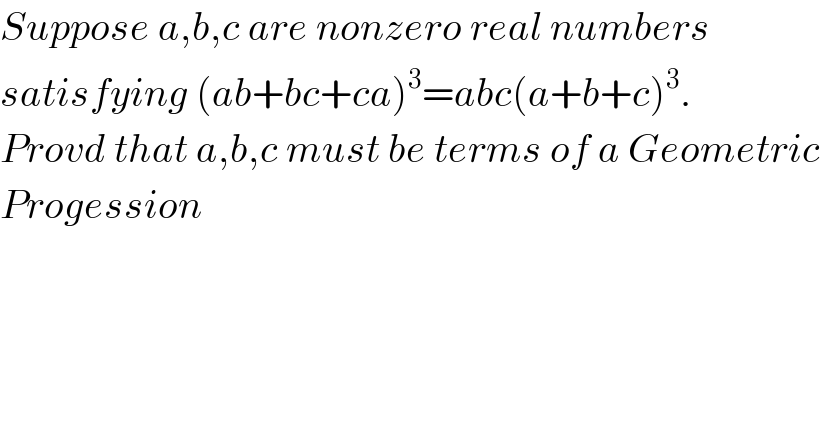
$${Suppose}\:{a},{b},{c}\:{are}\:{nonzero}\:{real}\:{numbers} \\ $$$${satisfying}\:\left({ab}+{bc}+{ca}\right)^{\mathrm{3}} ={abc}\left({a}+{b}+{c}\right)^{\mathrm{3}} . \\ $$$${Provd}\:{that}\:{a},{b},{c}\:{must}\:{be}\:{terms}\:{of}\:{a}\:{Geometric} \\ $$$${Progession} \\ $$$$ \\ $$
Commented by Snail last updated on 08/Dec/20
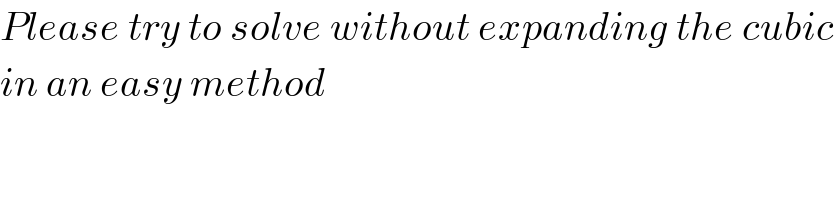
$${Please}\:{try}\:{to}\:{solve}\:{without}\:{expanding}\:{the}\:{cubic} \\ $$$${in}\:{an}\:{easy}\:{method} \\ $$
Commented by Dwaipayan Shikari last updated on 08/Dec/20
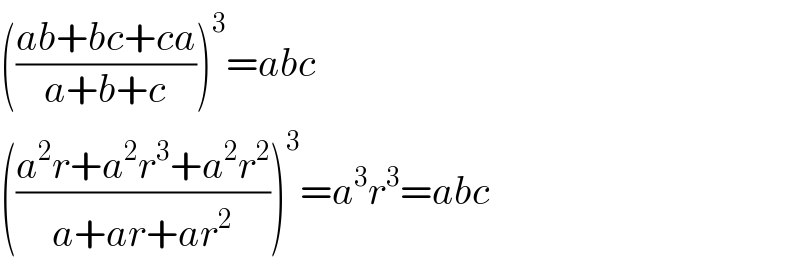
$$\left(\frac{{ab}+{bc}+{ca}}{{a}+{b}+{c}}\right)^{\mathrm{3}} ={abc} \\ $$$$\left(\frac{{a}^{\mathrm{2}} {r}+{a}^{\mathrm{2}} {r}^{\mathrm{3}} +{a}^{\mathrm{2}} {r}^{\mathrm{2}} }{{a}+{ar}+{ar}^{\mathrm{2}} }\right)^{\mathrm{3}} ={a}^{\mathrm{3}} {r}^{\mathrm{3}} ={abc} \\ $$
Commented by Snail last updated on 08/Dec/20

$${This}\:{is}\:{thorrowly}\:{wrong}\:...{because}\:\:{u}\:{can}'{t} \\ $$$${assume}\:{they}\:{are}\:{inG}.{P}\:.....{u}\:{have}\:{to}\:{prove}\:{that} \\ $$$${u}\:{have}\:{proved}\:{the}\:{vice}-{versa}\:{result}......{Try}\: \\ $$$${another}\:{way} \\ $$
Answered by Dwaipayan Shikari last updated on 08/Dec/20

$${b}={ka} \\ $$$${c}={ta} \\ $$$$\left({ab}+{bc}+{ca}\right)^{\mathrm{3}} =\left({a}^{\mathrm{2}} {k}+{a}^{\mathrm{2}} {kt}+{a}^{\mathrm{2}} {t}\right)^{\mathrm{3}} ={a}^{\mathrm{6}} \left({k}+{t}+{kt}\right)^{\mathrm{3}} \\ $$$$\left({a}+{b}+{c}\right)^{\mathrm{3}} ={a}^{\mathrm{3}} \left({k}+{t}+\mathrm{1}\right) \\ $$$$\left({k}+{t}+{kt}\right)^{\mathrm{3}} ={kt}\left({k}+{t}+\mathrm{1}\right)^{\mathrm{3}} \:\:\:\:\:\:\:{k}=\frac{{p}}{{t}} \\ $$$$\Rightarrow\left(\mathrm{1}+\frac{{kt}−\mathrm{1}}{{k}+{t}+\mathrm{1}}\right)^{\mathrm{3}} ={kt} \\ $$$$\Rightarrow\left(\mathrm{1}+\frac{{p}−\mathrm{1}}{{p}\left({t}+\frac{\mathrm{1}}{{t}}\right)+\mathrm{1}}\right)^{\mathrm{3}} ={p}\Rightarrow\frac{{p}−\mathrm{1}}{{p}\left({t}+\frac{\mathrm{1}}{{t}}\right)+\mathrm{1}}=\sqrt[{\mathrm{3}}]{{p}}−\mathrm{1}\:\:\:\:\:\:\:\:{p}={m}^{\mathrm{3}} \\ $$$$\Rightarrow\frac{{m}^{\mathrm{2}} +{m}+\mathrm{1}}{{m}^{\mathrm{3}} \left({t}+\frac{\mathrm{1}}{{t}}\right)+\mathrm{1}}=\mathrm{1}\Rightarrow{m}^{\mathrm{2}} +{m}={m}^{\mathrm{3}} \left({t}+\frac{\mathrm{1}}{{t}}\right)\Rightarrow{m}+\mathrm{1}={m}^{\mathrm{2}} \left({t}+\frac{\mathrm{1}}{{t}}\right) \\ $$$${t}=\frac{{m}+\mathrm{1}+\sqrt{\left({m}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}{m}^{\mathrm{4}} }}{\mathrm{2}{m}^{\mathrm{2}} }\:\:{k}={p}\left(\frac{{m}+\mathrm{1}−\sqrt{\left({m}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}{m}^{\mathrm{4}} }}{\mathrm{2}{m}^{\mathrm{2}} }\right) \\ $$$${p}=\mathrm{1} \\ $$$$\:{b}={a}\frac{\mathrm{1}}{\left(\frac{{m}+\mathrm{1}+\sqrt{\left({m}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}{m}^{\mathrm{4}} }}{\mathrm{2}{m}^{\mathrm{2}} }\right)}\:,\:{c}={a}\left(\left(\frac{{m}+\mathrm{1}+\sqrt{\left({m}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}{m}^{\mathrm{4}} }}{\mathrm{2}{m}^{\mathrm{2}} }\right)\right) \\ $$$$ \\ $$
Commented by Snail last updated on 08/Dec/20

$${Quite}\:{good} \\ $$
Commented by Snail last updated on 09/Dec/20
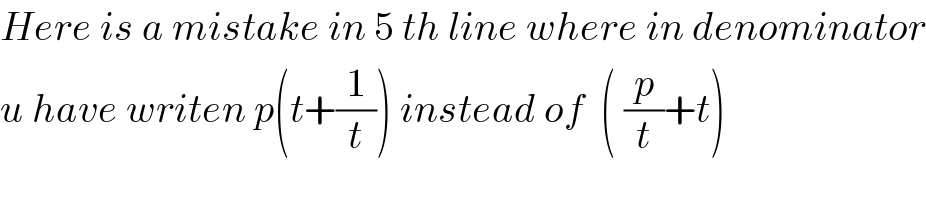
$${Here}\:{is}\:{a}\:{mistake}\:{in}\:\mathrm{5}\:{th}\:{line}\:{where}\:{in}\:{denominator} \\ $$$${u}\:{have}\:{writen}\:{p}\left({t}+\frac{\mathrm{1}}{{t}}\right)\:{instead}\:{of}\:\:\left(\:\frac{{p}}{{t}}+{t}\right) \\ $$
